|
Images animées et logiciel interactif Colette Girardot La géométrie se consacre à l'étude des objets de l'espace, de leurs propriétés et des relations qu'ils ont entre eux. Le langage Smalltalk quant à lui, est conçu sur le paradigme des objets. Donnons d'emblée un exemple : La classe Triangle préexiste, elle permet de créer autant de triangles que l'on veut, en jouant sur leurs propriétés (taille, couleur, caractère plein ou creux etc.). Chaque objet sera nommé et l'on pourra lui donner des ordres (appelés méthodes).
Dans la vie courante l'enfant perçoit un espace rempli d'objets par le biais de ses sens (la vue, le toucher, l'ouïe...). Yves Chevallard appelle cet espace : l'espace sensible. Le point, la droite, le carré n'y appartiennent pas. On les conçoit en mathématique de manière abstraite et idéale. Pourtant, l'enfant ne pourra accéder aux concepts mathématiques, qu'après avoir manipulé et construit de nombreux objets matériels avec du papier, un crayon, une règle, des ciseaux... Dans cet article nous montrons que l'outil informatique peut permettre à l'enfant de créer de objets géométriques, de les manipuler, d'agir sur eux et de changer leurs propriétés. Il va ainsi consolider ses représentations mentales des objets de l'espace géométrique, anticiper des successions d'actions, affiner et consolider sa pensée logique. Des logiciels simples, peuvent aider l'élève à visualiser des concepts mathématiques, en lui permettant d'amorcer ou de consolider, une construction mentale qui facilitera l'approche scolaire, parfois ingrate, du cours classique de mathématique. Les exemples développés concernent essentiellement les isométries du plan : translations, rotations et symétries par rapport à une droite ainsi que les propriétés des objets géométriques. Les étapes essentielles de l'approche didactique sont :
La première étape de la recherche a été la conception et la programmation d'un environnement de programmation orientée objet pour des enfants d'école primaire (maternelle et élémentaire). Le logiciel Smalltalk, un jeu d'enfants... s'appuie sur des situations de géométrie (translations, symétries, rotations...) et des classifications de verbes selon leur modèle de conjugaison. Les travaux s'inspirent de la pensée de Papert (l'enfant peut et doit programmer l'ordinateur) et de celle des fondateurs du langage Smalltalk, Adele Goldberg et Alan Kay. Nous allons envisager dans la deuxième partie de cet article, une utilisation possible des modules « objets divers » et « objets par morceaux » à l'école maternelle. L'enfant agit en cliquant sur des formes, sur des couleurs, sur des boutons symbolisant les symétries, les rotations, les translations, etc. A) L'IMAGE ANIMÉE POUR ENSEIGNER LA GÉOMÉTRIE AU COURS MOYEN 1) Un exemple pour le cours moyen. Comment un carré peut se transformer en colombe L'animation que nous décrivons ici utilise les logiciels KidPix et SlideShow.
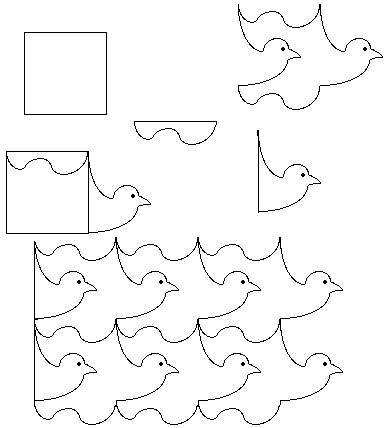
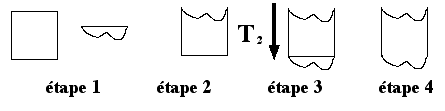
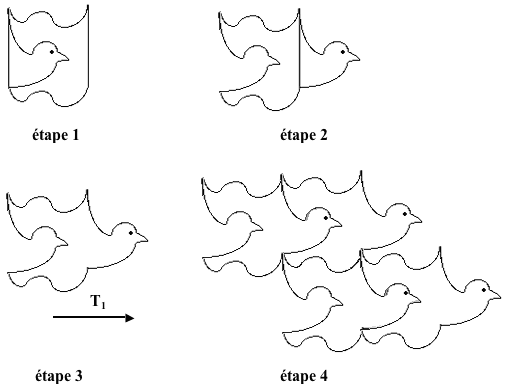
Les carrés colorés en couleurs vives apparaissent un par un, dans l'ordre indiqué. Ils engendrent un pavage par les deux translations T1 et T2.
Le carré va peu à peu se transformer en une forme différente qui pave. Les morceaux doivent être déplacés selon T1 et T2. La nouvelle forme pave et garde la même surface que le carré. Le morceau qui est découpé en haut, doit être impérativement placé en bas exactement selon T2.
Le même principe est repris mais cette fois-ci avec la translation T1.
La réalisation du dessin animé On utilise alors le logiciel SlideShow, qui va permettre de réaliser l'animation. Les différents dessins sont placés dans des camions et le temps d'affichage de chaque dessin sera très bref, pour créer le mouvement du dessin animé.
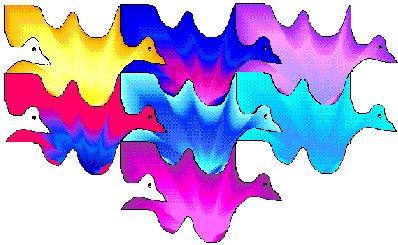
L'exploitation avec les élèves Il va de soit, que ce type de film est trop complexe à réaliser pour un élève. Dans ce cas particulier, c'est l'enseignant qui fait le film sur les pavages. Ce sera un film de motivation qui amènera l'élève à chercher d'autres dessins figuratifs qui pavent. Un carré découpé, dans du papier un peu rigide, des ciseaux, un peu de ruban adhésif et le tour est joué... L'enfant pourra fabriquer des poissons, des oiseaux des fleurs à partir d'un rectangle ou d'un carré. Il utilisera cette forme comme gabarit et réalisera de superbes pavages.
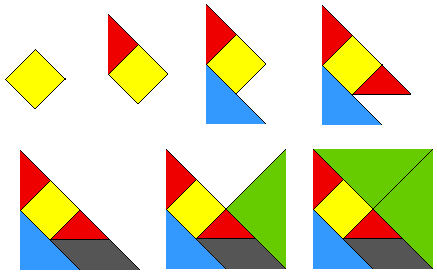
2) Un autre film pour le cours moyen : « le tangram » Un dessin animé (réalisé avec le logiciel SlideShow) construit sous nos yeux un carré avec les pièces du tangram.
Avec les mêmes pièces les enfants, émerveillés, voient ensuite se construire un cygne, un lapin, un personnage en ombre chinoise...
Le principe reste toujours le même, maintenant c'est l'enfant, qui construira et découpera un tangram dans du carton et qui essayera de réaliser des formes figuratives, il s'aidera ou non de la notice du véritable jeu chinois. Rappelons brièvement que les activités sur le tangram permettent d'aborder les isométries du plan, mais aussi l'homothétie, les mesures de surfaces et même les fractions !
4) Le début du scénario... Découvrons la syntaxe du langage Smalltalk :
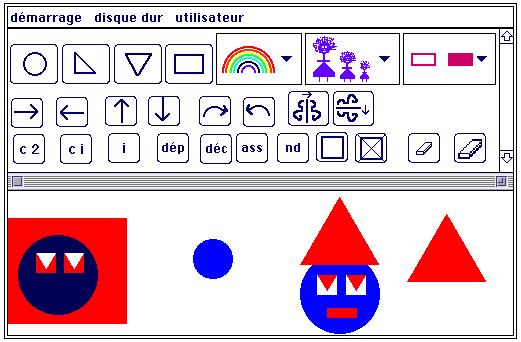
B) UTILISATION DU LOGICIEL « SMALLTALK UN JEU D'ENFANTS » À L'ÉCOLE MATERNELLE L'enfant de maternelle utilise les modules « objets divers » et « objets par morceaux » pour créer très rapidement des objets aux propriétés variées (forme, couleur, décoration etc.). L'enfant agit ensuite sur ces objets grâce à des boutons symbolisant les symétries, les rotations, les translations etc. Pour réaliser un projet précis, l'enchaînement des actions ne peut se faire au hasard. Comme en Logo, la suite logique des actions est primordiale. 1) Présentation des modules « objets divers » et « objets par morceaux » * Objets divers L'enfant, en cliquant sur le bouton « panda », crée un objet et le dépose où il veut sur l'écran. Il créera autant de pandas qu'il le désire, de même pour les éléphants, les ânes ou les petits trains. Il pourra exercer beaucoup d'actions sur ces objets (translations, rotations, symétries, inversion de couleurs...). Il les effacera, les déplacera, les décalquera à sa guise. Ce module peut être utilisé en maternelle, en CP ou au CE. Mais dans cet article, nous nous intéresserons surtout aux notions mathématiques qui doivent être introduites ou consolidées à l'école maternelle, en liaison avec les instructions officielles.
Le codage des actions...
* Objets par morceaux Dans les phases précédentes, l'enfant utilisait des dessins tout faits proposés par le logiciel. Maintenant, il crée lui-même de nouveaux objets en associant des cercles, des rectangles, des triangles dont il décide lui-même la taille, la couleur, le caractère vide ou plein. Il clique ensuite sur le bouton qui détermine l'action : rotation, symétrie, changement de couleur. L'enfant crée d'abord les objets puis il leur envoie des ordres. Nous nous intéressons ici aux propriétés des objets et à la création implicite de nouvelles classes. Ce module peut-être utilisé à l'école maternelle, mais ne doit surtout pas être confondu avec un logiciel de dessin, comme peut l'être l'excellent Kid-Pix.
2) Utilisation du logiciel en maternelle Les modules « objets par morceaux » et « objets divers » intéressent beaucoup les enseignants de maternelle. Les enfants, après avoir manipulé de vrais « blocs logiques » : triangles, rectangles, ronds, carrés, bleus, rouges, verts, grands ou petits, creux ou pleins, en fabriqueront eux-mêmes avec l'ordinateur, en énonçant les propriétés par oral : « Un grand triangle rouge creux, un petit carré vert plein... ». Toutes les notions rencontrées sont au coeur même des programmes de l'école maternelle, et ce n'est pas un hasard car elles sont le fondement de la pensée logique et mathématique de l'enfant.
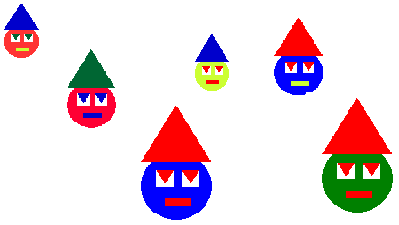
• Des classements d'objets en fonction de l'une de leurs qualités La notion de triangle est loin d'être évidente pour des enfants de petite et de moyenne section. La machine à créer des objets produirait ces formes à volonté, une fois imprimées et découpées, les enfants les manipuleront à nouveau et formeront la classe des triangles, des rectangles, des verts, des mauves... Le logiciel permet aussi de créer et d'inventer une multitude d'objets et de faire de nombreux classements. Avec des enfants plus âgés, en grande section, nous formons de nouvelles classes par association d'objets élémentaires en laissant libre cours à l'imagination et à la créativité des enfants. On obtiendra par exemple la classe des clowns :
Une fois créés, ces objets peuvent être de nouveau classés en sous-classes : les clowns avec une bouche rouge, avec un chapeau bleu, les petits clowns... On peut aussi réaliser des tableaux cartésiens en fonction de deux critères. • Des rangements d'objets en particulier grâce à des critères quantitatifs (plus grand, plus gros, plus large...) Les rangements correspondent à des relations d'ordre. Ils peuvent avoir lieu - sur les objets élémentaires
- sur les objets fabriqués
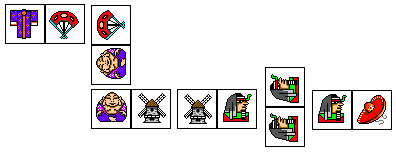
• Pratiquer des jeux à règles - jeu à une différence et une seule... Le jeu à une différence et une seule est un jeu très classique. Il est particulièrement intéressant d'y jouer avec l'ordinateur, car l'enfant devra anticiper les propriétés de l'objet, sans le voir, avant de le poser sur l'écran. Il ne dispose pas de l'objet tout construit sous les yeux.
- fabrication d'un jeu de dominos pour jouer sur l'écran Une telle activité peut s'inscrire dans un projet de classe. Au préalable les enfants auront joué avec des dominos classiques ou imagés. Dans une première étape le logiciel permettra de fabriquer les pièces d'un jeu par association de deux carreaux. Pour des enfants très jeunes, c'est l'enseignant qui le fera. Dans une deuxième étape, ce sont les enfants qui déplaceront les dominos sur l'écran. Bien sûr, les enfants pourront imprimer, découper et coller leurs dominos sur des rectangles de carton, pour jouer avec les objets réels.
• L'enfant peut utilement travailler sur les sériations et les rythmes Comme pour les dominos ou les papiers peints, réaliser avec l'ordinateur ne dispense aucunement l'enfant, d'une action préalable avec des objets matériels : perles, formes découpées dans du papier coloré, tampons ou pochoirs... L'action avec l'ordinateur sera beaucoup plus abstraite, car à nouveau il faudra anticiper avant de créer... - continuer une frise commencée par l'enseignant... Il s'agit ici de continuer avec le logiciel une succession régulière d'objets.
- continuer l'exercice verticalement... L'exercice se complexifie considérablement : il met en oeuvre deux dimensions, et fait apparaître verticalement une périodicité dans la succession des couleurs : vert, rose, bleu.
- créer un algorithme mettant en oeuvre symétries et translations... Dans les deux exercices précédents la périodicité se faisait sur les propriétés des objets affichés (triangle, carré, rond horizontalement et rose, rouge, bleu verticalement), nous pouvons imaginer un exercice portant sur la régularité des actions (alternance de symétries et de translations). Les enfants doivent continuer le carrelage commencé par l'enseignant. Cette activité nous semble assez difficile et est destinée à des enfants de grande section.
• L'enrichissement des observations qui préparent à la géométrie Les enfants de moyenne et de grande section peuvent sans aucune difficulté utiliser « Objets divers » pour fabriquer des papiers peints. Les programmes de l'école maternelle insistent beaucoup sur l'organisation de l'espace (dessus, dessous, au-dessus, au-dessous, à gauche, à droite). L'analyse et la fabrication de papiers peints peut être l'occasion rêvée de travailler ces notions dans le plan, tout en offrant la possibilité d'entrevoir des notions difficiles comme la symétrie.
Pour conclure En géométrie, le logiciel permet à l'enfant des situations de recherche et de découverte. Il permet une meilleure structuration de l'espace-plan. De réels progrès sont possibles au niveau de la logique, du raisonnement et des classifications. Les enfants peuvent aussi comprendre quelques notions sur le fonctionnement de l'ordinateur. Les enfants de moins de cinq ans agissent dans ce monde d'objets virtuels avec beaucoup d'aisance et surtout ils sont amenés à anticiper les propriétés et les actions avant d'agir. CONCLUSION La problématique de l'introduction de l'informatique dans l'enseignement a toujours suscité de nombreuses polémiques. Les enseignants sont souvent très déçus par la qualité pédagogique des logiciels qu'ils trouvent sur le marché. Ils se sentent prisonniers, d'une approche qui n'est pas la leur. Ils savent adapter et modifier un manuel scolaire à leur sensibilité et à leurs besoins, tandis qu'ils sont prisonniers de logiciels conçus par d'autres. Dans le meilleur des cas, on les autorise à régler le niveau de difficulté ou à connaître les erreurs de l'élève et son cheminement... À l'opposé, les exemples que nous présentons permettent à l'enseignant de créer des documents multimédias d'une manière souple et évolutive. Ces documents correspondent à ses besoins et à sa sensibilité pédagogique. Rien n'empêche les élèves eux-mêmes, par la suite, de modifier le document ou de l'enrichir. La créativité et l'imagination des enfants sont sans cesse sollicitées. Chemin faisant, les concepts fondamentaux des isométries du plan vont se mettre en place, ce qui aidera bien sûr à comprendre la présentation plus abstraite et plus ingrate qu'ils auront au collège ou au lycée. Ces logiciels sont un auxiliaire précieux pour faire surgir des situations de recherche. Remarquons que l'utilisation de l'ordinateur n'a en aucun cas dispensé les élèves d'une manipulation concrète et manuelle : papier, crayon, calque, ciseaux, imprimante et rétroprojecteur ont été absolument indispensables. Les enfants en situation de recherche, ont enrichi le projet pédagogique, leur imagination a souvent dépassé la créativité de l'adulte concepteur du logiciel. Les interactions entre les enfants sont essentielles : en petit groupe ou en synthèse collective, ils ne cessent de s'interpeller, de se questionner, de s'expliquer et de se corriger les uns les autres. Les informations, les critiques, les suggestions sont formulées dans un langage qui est le leur, différent de celui de l'adulte, donc bien mieux adapté à leur niveau de compréhension. Bien sûr, les enfants n'ont pas tout inventé spontanément. Nous étions là, pour poser des questions, aider à la structuration, et parfois les conseiller et les emmener le plus loin possible. Les enfants à partir de leur réalisation sur l'écran, font des découvertes mathématiques intéressantes et surtout ils sont capables de les analyser et de se construire de nouveaux outils mathématiques. Chemin faisant, les enfants « commencent à entrevoir » de nombreuses propriétés des groupes d'isométries. Il va de soi que nous posons des jalons pour le collège et le lycée où ces notions seront approfondies. Elles seront d'autant mieux comprises, qu'elles auront été vécues par les enfants en maternelle et au cours moyen. Les isométries sont présentées de manière dynamique. L'enfant est libéré, grâce à l'ordinateur de la partie fastidieuse du travail : un superbe papier peint, un merveilleux pavage peuvent se fabriquer en quelques minutes, voire en quelques secondes... Bien sûr ce n'était pas notre motivation prioritaire, mais l'esthétique des réalisations a créé de grandes fiertés et a contribué à la motivation générale. Remerciements très chaleureux à Christophe Gentil pour ses précieux conseils et ses encouragements à écrire l'article et pour l'aide en programmation Flash. Colette Girardot Annexe Quelques animations Flash® proposées aux élèves, Si vous ne pouvez pas lancer les animations sur votre ordinateur, vous pouvez télécharger Flash Player gratuitement : • PC • Mac Bibliographie Artigue Michèle, (1990). Analyse des processus d'enseignement en environnement informatique, Actes de l'Université d'été informatique et enseignement de la géométrie, IREM de Toulouse, p. 125-150. APMEP de Haute-Normandie, Élisabeth Hébert (2000). Math en scène, 22 articles pour se repérer dans l'exposition maths 2000. Bulletin de l'APMEP n° 419. Balacheff Nicolas, (1994). La transposition informatique, un nouveau problème pour la didactique des mathématiques, In Artigue et al. (eds.), Vingt ans de didactique des mathématiques en France, La pensée sauvage éditions, Grenoble, p. 364-370. Bettinelli Bernard, (2001). Actions géométriques avec un ensemble de gabarits. Repères n° 43, TOPIQUES éditions Metz, p. 5-27. Chevallard Juillien, (1991). Autour de l'enseignement de la géométrie au collège. Revue Petit x, n° 27, IREM de Grenoble, p. 41-76. Girardot Colette (1994). Recherches entreprises par les enseignants-chercheurs de l'IUFM de Paris, Séminaire de recherche n° 8, Service de publication et d'Édition de l'IUFM de Paris, p. 31-42. Girardot Colette, Borne Isabelle, Durand Raymond (1996). « Smalltalk un jeu d'enfants... », Revue de l'EPI n° 83 sept. 1996, p. 65-71. Girardot Colette, (1997). Smalltalk, un jeu d'enfants, Thèse didactique de l'informatique, Paris 7, sujet : Les concepts spécifiques aux langages à objets peuvent-ils servir de support à l'initiation à l'informatique chez les enfants de 8 à 11 ans ? Girardot Colette, (1996). L'enfant et l'ordinateur, Actes du Séminaire Européen de l'OMEP 24/27 octobre 1996, OMEP-FRANCE sous l'égide de l'UNESCO. PANEL de Jeannine Deunff (Inspectrice générale de l'Éducation nationale). Grandbastien Monique, (1996). Introduction, Sciences et techniques éducatives, Vol. 3, n° 2, numéro spécial géométrie, Hermès, p. 145-155. Papert Seymour, (1980). Mindstorms : Children,Computers and powerful ideas, Basic Books, New-York. Papert Seymour, (1981). Jaillissement de l'esprit (Ordinateurs et apprentissage), Flammarion. Piaget Jean, (1972). La formation du symbole chez l'enfant, Actualités pédagogiques et psychologiques, Delachaux et Nieslé. Raba Raoul (1998). ZOO Mathématique, Éditeur : ACL, Les Éditions du Kangourou, Paris. ___________________ |




 3) Comment le carré peut-il se transformer en chat ?
3) Comment le carré peut-il se transformer en chat ?