L'équipe

Introduction

   Paraschool est le leader français actuel en matière de soutien scolaire à distance avec plus de 250 000 utilisateurs, dont 5 000 utilisateurs privés et le reste dans le cadre de contrats avec des établissements scolaires. En 2001, Paraschool a voulu mettre en place un système évolutif capable de proposer des chemins pédagogiques « intelligents », adaptés à chaque élève.

   Il est rapidement apparu que la technique d'optimisation par colonie de fourmis (OCF) [DoDi97] [BDT99] [BDT00] semblait pouvoir s'appliquer directement au problème grâce au fait que les différents items pédagogiques composant le logiciel Paraschool pouvaient s'organiser sous forme d'un graphe qui serait parcouru par les 250 000 élèves inscrits chez Paraschool, constituant non plus une fourmilière, mais une hommilière.

   Une première version de l'algorithme [SeCo03] [SJB03] [SLC03] a donc été mise en place sur cette base, mais les premiers tests en grandeur nature ont montré que le paradigme maintenant bien connu de l'OCF était difficilement transposable au système de Paraschool, car une hommilière ne présente pas les mêmes caractéristiques qu'une colonie de fourmis artificielles. Le test du premier prototype avait fait l'objet d'un article dans l'EPI Application de l'optimisation par colonies de fourmis à la structuration automatique de parcours pédagogiques, on y trouvera une bonne description de l'optimisation par colonies de fourmis, ainsi que le concept de base de ce projet.

   Dans cette phase d'amélioration du paradigme, le niveau des items et des élèves doit être évalué afin de pouvoir proposer à l'élève des exercices adaptés à son niveau (sans ça, rien n'empêche au système de proposer des exercices très difficiles ou très faciles). L'équipe pédagogique pourrait noter les différents items à partir de leur propre expérience d'enseignants. Mais l'entreprise est fastidieuse (des milliers d'items) et aussi subjective. Une solution a été trouvée dans le monde des échecs avec le système de notation Elo.

   Après une description actualisée de l'hommilière de Paraschool et de ses différences avec les algorithmes d'OCF, une description succincte de l'algorithme sera faite. Ensuite, dans la logique d'individualisation de l'algorithme, la notation Elo sera décrite dans la section 3 et appliquée à Paraschool dans la section 4. Les résultats sur trois années seront présentés et analysés, avant de terminer sur les perspectives.

I. Nouveau paradigme : l'Hommilière

I.a. Cahier des charges

   Le site Paraschool est un site de soutien scolaire qui propose des compléments pédagogiques, des fiches de cours et des exercices. Il est fondé sur des principes comportementaux : le résultat de l'exercice traité est tout de suite présenté à l'élève. En cas d'erreur, un mécanisme de remédiation intervient : l'élève peut être alors redirigé vers le point du cours non assimilé. Cette philosophie est bien adaptée à l'apprentissage assisté par ordinateur, par opposition au constructivisme où le professeur est censé mettre l'élève en présence de situations et d'éléments qui doivent lui permettre de construire ses propres connaissances.

   L'abonnement à Paraschool permet à l'élève d'accéder à une ou plusieurs matières et d'avoir accès à une assistance en direct, par mail ou par chat avec un professeur. L'essentiel du contenu concerne les élèves de collège-lycée et se concentre sur plusieurs matières telles que les mathématiques, la physique, le français, l'économie...

   À la fin d'une session, les résultats sont enregistrés et quelques courbes, assorties de commentaires pédagogiques, permettent à l'élève de suivre sa propre progression. L'élève a deux types de navigation à sa disposition :

• Navigation libre : Passé le choix de la matière à travailler (mathématiques par exemple), l'élève se voit proposer une liste de chapitres correspondant à son niveau, dans lesquels il trouvera trois catégories représentant des entités pédagogiques ou items :
  • Points de cours : Ce sont des rappels de cours validés par des tests d'application directe du cours.
  • Savoir-faire : Ces items représentent les méthodes utiles à connaître pour une bonne utilisation des notions de cours. C'est la vision pratique du cours.
  • Exercices : il faut valider les exercices pour valider le chapitre.
  Chaque item se termine par une validation interactive, la plupart du temps sous forme de questionnaire à choix multiples. Le résultat est analysé et commenté. En cas d'échec, une remédiation est proposée. En cas de réussite, l'élève a la possibilité de revenir sur les différents menus pour choisir le prochain item qu'il va effectuer, sans contrainte de thème, de cursus ou de matière.
• Navigation guidée : l'étudiant peut également, dans un chapitre donné, se laisser guider interactivement le long d'un chemin (une suite d'items) prédéfini par l'équipe pédagogique. Cette possibilité était implémentée de manière linéaire et déterministe. C'est ici qu'intervient le système mis en place : l'hommilière aura la charge de proposer une suite « intelligente » à l'exercice qui vient d'être terminé, l'objectif étant d'optimiser individuellement l'apprentissage de l'élève sur le chemin pédagogique proposé.

   Paraschool cherchait une technique pour rendre son site plus attrayant et plus efficace du point de vue pédagogique. L'objectif du système est donc double :

• Adaptativité : Tout d'abord, il faut que le site réagisse dynamiquement et puisse présenter un contenu adapté à chaque utilisateur mais aussi à la collectivité (cas d'un professeur en salle machines désirant que les élèves travaillent sur un point précis).
• Émergence : Ensuite, le système doit permettre de faire émerger de nouveaux chemins correspondant à une réalité pour les élèves, et auxquels l'équipe pédagogique de Paraschool n'aurait pas forcément pensé.

I.b. Première solution : l'Optimisation par Colonies de Fourmis (OCF)

   Ce sont ces caractères d'émergence et d'adaptabilité qui ont suggéré l'utilisation du paradigme OCF dans le cas de Paraschool, pour tenter de faire émerger des chemins pédagogiques :

• Structure du système de Paraschool : le logiciel Paraschool a été implémenté pour une utilisation via Internet. Il utilise donc des pages et des liens hypertextes que l'on peut structurer en graphe, environnement dans lequel les fourmis artificielles ont déjà montré dans de nombreux cas leur aptitude à trouver un chemin optimal. Chaque solution est bien sûr dividuelle et l'équipe pédagogique s'intéressera aux mouvements de masse.
• Un nombre suffisant d'utilisateurs : un autre avantage du système Paraschool est le très grand nombre d'élèves amenés à utiliser le logiciel (250 000). Cela permet – cas quasiment ¹ unique jusqu'à présent – de considérer chaque utilisateur comme une fourmi virtuelle.

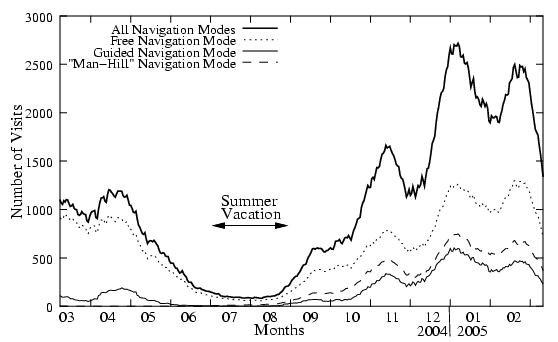Figure 1 : Nombre de passages sur une année sur le site de Paraschool
en fonction du mode de navigation (vérification a posteriori).


• Un comportement aléatoire possible : la navigation libre permet à l'utilisateur de ne pas se restreindre aux propositions faites par le système et donc de pouvoir choisir son propre enchaînement d'items, proposant ainsi de nouveaux chemins au système.

   Dans le cas habituel, on a recours à un grand nombre de fourmis artificielles dont on essaye de modéliser le comportement, ce qui pose bien sûr le problème de trouver une bonne modélisation. Dans le cas présent, il est donc possible d'envisager d'associer bijectivement une fourmi à un élève avec l'espoir de voir apparaître dans le logiciel Paraschool des comportements d'émergence et d'auto-organisation fondés sur le comportement de l'ensemble des élèves.

I.c. Adaptations

I.c.1. Premières adaptations

   Après plusieurs mois de tests sur des petites expériences fictives puis de tests sur le système de Paraschool, il s'est avéré qu'associer bijectivement une fourmi à un utilisateur demande des modifications par rapport au paradigme standard de l'Optimisation par Colonies de Fourmis :

• Comportement : habituellement, les fourmis artificielles sont programmées pour résoudre un problème donné. Dans notre cas, les élèves humains ne suivent pas un algorithme en particulier. Ils vont où ils veulent et les seules influences possibles passent par les suggestions faites par le système ou par leurs professeurs. Ce comportement ressemble plus ou moins au comportement possiblement erratique des vraies fourmis.
• Activité : les fourmis artificielles sont constamment actives dans tout l'environnement, à la différence des élèves qui ont des périodes de repos (vacances...) et qui n'étudient les différents thèmes qu'à des moments précis de l'année. Une évaporation des phéromones basée sur le temps effacera toute l'information portée par les arcs d'un domaine (les vecteurs en seconde, par exemple) qui n'aura pas été visité depuis l'année précédente, ce qui n'est pas souhaitable.
• Contraintes particulières : des contraintes qui n'auraient aucun sens avec les fourmis artificielles s'appliquent sur les élèves. En effet les fourmis artificielles ne se plaindront jamais, par exemple, de refaire plusieurs fois le même exercice. L'élève, lui, reconnaîtra tout de suite un exercice déjà proposé et risque de s'agacer en cas de répétition.
• Altruisme : les colonies de fourmis naturelles et autres insectes sociaux se comportent de manière altruiste en ce qui concerne la colonie, jusqu'à se battre pour elle jusqu'à la mort. L'avenir de la colonie entière est plus importante que celui d'un seul individu, et de ce fait, certaines fourmis n'hésitent pas à aller explorer des zones lointaines pour le bien de la communauté. Ces comportements, implémentables avec des fourmis artificielles, sont rarement observés chez les humains... Il y a peu de chance qu'un élève n'aille jamais explorer une partie obscure du graphe Paraschool pour le bien de ses copains de classe.
• Personnalisation :Les fourmis jouent à ce point la carte de l'altruisme qu'elles sont pratiquement indifférenciées dans leurs castes respectives. À l'inverse, l'humain est intrinsèquement individuel (cf. la célèbre exclamation « Je ne suis pas un Numéro, je suis un homme libre !!! » hurlée par Patrick Mc Goohan dans la série culte Le Prisonnier). Entre un système qui considèrera chaque élève de manière identique et un autre, qui sera capable de personnaliser l'interface et le parcours pédagogique en fonction de l'élève derrière l'écran, tous les être humains préfèreront le deuxième.

   Du fait de ces différences majeures, il est nécessaire d'apporter plusieurs changements au paradigme original pour qu'il s'applique aux hommilières.

I.c.2. De l'évaporation à l'érosion

   Le premier changement testé concerne l'évaporation des phéromones. Elle joue un rôle capital car elle permet à la colonie de fourmis de disposer en permanence d'informations constamment remises à jour. Dans un système basé sur une fourmilière artificielle, il est donc important de simuler une forme d'évaporation pour éviter que le système ne reste bloqué dans un optimum local et lui offrir ainsi une adaptabilité.

   Les premiers tests en grandeur nature sur le logiciel Paraschool ont montré que l'évaporation temporelle des OCF n'était vraiment pas adaptée aux hommilières. Sur quelle base évaporer les phéromones ? Sur une base journalière, hebdomadaire, mensuelle ?

   Lors des premiers tests, il s'est avéré que les parties du graphe non utilisées pendant un certain temps (vacances scolaires, par exemple) perdaient rapidement l'information collectée et tout était à refaire. D'un certain point de vue, cette perte d'information n'est pas forcement si pénalisante. En effet, d'une année sur l'autre, les programmes changent ainsi que les élèves. Mais d'un point de vue pédagogique, le système prend du temps à se mettre en place et donc à devenir efficace.

   La méthode explorée est donc de remplacer le phénomène d'évaporation par un phénomène d'érosion, qui se produit à l'occasion du passage d'un élève sur un noeud et non plus par rapport au temps écoulé. L'évaporation n'est plus globale, mais locale : lorsqu'un élève aura validé un item A et suivra un arc vers un item B, tous les arcs sortant de l'item A seront érodés. Les arcs non suivis paieront de la valeur de l'érosion le fait de ne pas avoir été choisis, tandis que l'arc suivi (vers B), érodé lui aussi, verra les valeurs des phéromones qu'il porte modifiées par le succès ou l'échec à l'item B.

   Le nouveau terme érosion a été choisi car la décrémentation du niveau de phéromone n'a lieu que lors du passage d'un élève sur un noeud. Cette érosion amène l'avantage de ne pas perdre l'information durant les périodes d'inactivité tout en conservant un équivalent d'évaporation pour les arcs non sélectionnés.

I.c.3. Phéromones multiplicatives

   Le principe de stigmergie utilisé par les fourmis veut que les informations laissées sur le graphe soient à la disposition de tous, pour que des trajets optimaux finissent par émerger dans l'environnement. Mais ceci ne tient absolument pas compte de l'individualité des élèves. Comment réduire la probabilité pour un élève de retomber sur un exercice qu'il a déjà fait ? Comment tenir compte des « devoirs » qu'un professeur lui aura donné ? Comment tenir compte de son niveau ? Comment faire pour que le système offre une interaction personnalisée avec un élève particulier ?

   Une solution consiste à utiliser un nouveau type de phéromones inconnues chez les fourmis : une phéromone multiplicative, une sorte d'exhausteur ou d'inhibiteur d'odeur présente dans l'environnement, associé à chaque élève. Un exemple simple est la phéromone multiplicative d'historique (cf. infra). Si, sur tous les arcs pointant vers un noeud validé, on dépose une une phéromone multiplicative d'historique d'une valeur de 0.5, les arcs pointant vers ce noeud deviendront deux fois moins attrayant pour cet élève.

   On pourra parler de phéromone multiplicative si celle-ci s'estompe au cours du temps (ou au cours des visites, suivant les cas). L'élément neutre pour la multiplication étant 1, l'évaporation d'une phéromone multiplicative la ramènera progressivement à 1. Si l'on utilise une évaporation temporelle, calculée pour s'estomper au fur et à mesure que la mémoire de l'élève s'estompe aussi, lorsque la phéromone d'historique sera revenue à 1, l'élève aura alors aussi oublié l'exercice et pourra le faire à nouveau sans désagrément.

   Inversement, ce genre de phéromone personnelle (et individualiste) permet de faire de la remédiation de manière subtile : si l'on détecte dans un exercice de physique que l'élève a échoué parce qu'il a fait une erreur en trigonométrie, le système pourra insidieusement donner la valeur 2 à une phéromone multiplicative individuelle de remédiation sur tous les arcs amenant à des exercices contenant de la trigonométrie (phéromone agenda). Si l'élève se trouve un jour face à un tel arc, la probabilité que le système le lui propose sera alors doublée. On peut noter qu'il sera intéressant de ramener la valeur de cette phéromone à 1 par érosion, et pas par évaporation, car cela reviendrait à supprimer les remédiations sans que l'élève n'ait effectué l'exercice. Il validerait en quelque sorte les remédiations « à l'ancienneté ».

   Comme on le voit, ces phéromones individuelles multiplicatives (n'existant pas dans l'OCF) permettent de personnaliser le parcours de l'élève de manière très fine et subtile. Deux élèves au passé différent, placés côte à côte et démarrant du même exercice se verront proposer des items différents suivant leurs interactions passées avec le système.

I.d. L'Hommilière

   Au fur et à mesure que l'on modifie le paradigme OCF pour l'adapter aux élèves humains, la question de savoir si nous sommes toujours face à un paradigme OCF devient de plus en plus pertinente.

   Les petites différences sont importantes, mais ce qui fait pencher la balance est l'objectif. En effet dans le paradigme des OCF, le but est de trouver un seul et unique chemin (le plus court) pour optimiser le temps de parcours de toutes les fourmis. Dans l'application présentée, c'est tout le graphe qui se trouve optimisé, ainsi que les valeurs des phéromones multiplicatives individuelles. À la fin, chaque élève se verra attribuer un chemin adapté aux paramètres globaux de Paraschool, mais aussi à ses paramètres personnels. Le cadre est toujours de l'optimisation, mais les buts à atteindre sont différents. Le paradigme de l'hommilière est beaucoup plus proche des fourmilières naturelles en ce sens que son but est d'optimiser globalement l'ensemble du graphe. Cette optimisation se situerait entre l'orientation d'utilisateurs sur le parcours de site web [LMV03] et l'optimisation par colonie de fourmis. La différence provient de ce que le moteur permettant l'évolution se base sur le comportement d'êtres humains, peu altruistes et ayant besoin de se sentir singuliers, avec les modifications nécessaires qui s'en suivent.

II. Application

   Le parcours d'un utilisateur prend cette forme : dans un niveau, l'élève choisit une matière, puis un thème. Le système lui propose alors une liste d'items parmi lesquels l'élève en choisit un qu'il va travailler. Une fois l'item en cours terminé et que son résultat a été affiché, le système évalue les liens hypertextes sortants grâce aux informations stockées sur ces liens (phéromones globales additives déposées par les élèves précédents, affinées par les phéromones individuelles multiplicatives citées ci-dessus...) pour être en adéquation avec le niveau de l'utilisateur et les objectifs pédagogiques de Paraschool. Grâce à cette évaluation, le système fait une petite sélection d'arcs pour les proposer à l'utilisateur, propositions qu'il n'est d'ailleurs pas obligé de suivre.

II.a. Paramètres Globaux

   Ces paramètres vont servir au système à donner la direction principale. La fonction d'évaluation des arcs va les utiliser pour faire un compromis entre la pédagogie et la collectivité.

II.a.1. Poids pédagogique

   Dans l'hommilière Paraschool, même si le résultat souhaité est l'émergence de bons chemins, il faut aussi tenir compte de la pédagogie. Ainsi les arcs sont initialisés par l'équipe pédagogique en utilisant des poids. Ces poids représentent la vision des professeurs sur les chemins pédagogiques. Chaque poids représente la valeur pédagogique d'un arc. Plus ce poids est important, plus l'arc concerné sera avantagé pour être sélectionné.

   À chaque fois qu'un professeur créé un nouveau thème, il lui est demandé de réfléchir à la structure du graphe relatif au thème ainsi qu'aux poids pédagogiques qu'il va associer à chaque lien. En l'absence de phéromones, seul ce poids pédagogique est existant. Ainsi les poids pédagogiques vont constituer la vision initiale des chemins pédagogiques. Les phéromones auront pour but de modifier cet environnement pour qu'il s'adapte aux utilisateurs.

II.a.2. Phéromones

   Ce sont les informations stigmergiques ² qui vont aider les autres élèves à se déplacer dans l'environnement pédagogique. Elles sont déposées sur les arcs et symbolisent le taux de réussite à l'item pointé en suivant cet arc. Il y a deux types de phéromones : φ⁺ pour les phéromones symbolisant le succès et φ^– pour l'échec. Ainsi lorsque, pour proposer une suite, le système regarde les informations présentes sur un arc entre A et B, il a une estimation à l'instant donné du taux de réussite des élèves à l'item B en provenance de l'item A.

II.b. Adaptation à l'individu

   Il faut maintenant que le système évolutif s'adapte à l'élève en particulier. Les poids et phéromones évoqués jusqu'ici sont des facteurs globaux dits collectifs : ils concernent l'ensemble des élèves et représentent les informations qu'ils vont utiliser pour construire leur cheminement.

   Les facteurs individuels que l'on peut prendre en compte sont nombreux (préférences, excellence, agenda de travail, etc.). Pour cette raison, plusieurs phéromones individuelles peuvent être implémentées. Ces informations vont teinter, individuellement, le parcours global proposé par l'hommilière en modifiant les valeurs des phéromones globales par un facteur multiplicatif. Ce sont encore des phéromones car elles sont déposées sur l'arc et s'évaporent de la même manière que les phéromones collectives. La seule différence est que l'information qu'elles implémentent ne sera utilisée que par l'élève qui l'aura déposé.

II.b.1 Poids historique

   La phéromone d'historique (φ_h) dépend d'un item et d'un utilisateur et est utilisée comme un coefficient multiplicatif sur la dose de phéromones globale portée par les arcs. Initialement, la phéromone historique est fixée à 1 et donc n'affecte pas la dose de phéromone présente sur les arcs. Lorsqu'un élève réussit un exercice, la phéromone historique est mise à une valeur de 0,5. La phéromone agissant comme facteur multiplicatif, si l'élève a la possibilité de revenir sur l'item en question, la valeur de l'arc y menant sera divisée par 2, ce qui signifie que l'arc aura moins de chances d'être sélectionné à nouveau par le système pour être proposé à l'élève.

II.b.2. Poids agenda

   À l'inverse de la phéromone d'Historique, le poids agenda est un facteur multiplicatif poussant l'utilisateur à aller vers certains items soit qui ont été conseillé par un professeur, soit que le système juge nécessaire d'y passer.

II.b.3. Poids Niveau

   L'objectif de ce paramètre est de donner un niveau à l'élève pour aider à le guider vers des exercices d'une difficulté correspondant à sa force. C'est ici que va intervenir la notation Elo, décrite dans la section suivante.

II.c. Fitness des arcs

   Une fois la formalisation faite, les paramètres sont utilisés dans la fonction d'évaluation qui va permettre de noter tous les arcs sortants. La note déterminée (appelée fitness) permettra ensuite aux procédures de sélection de choisir quelques arcs parmi l'ensemble des possibilités. L'évaluation est importante car c'est elle qui détermine le type de chemins que l'on souhaite voir émerger.

• Remarque : le terme de fitness, tiré des algorithmes évolutionnaires, a été utilisé pour représenter la note des arcs, car à l'issue d'un item, les arcs entrent en compétition pour être choisis par un opérateur de sélection standard dans les algorithmes évolutionnaires.

• Adéquation à un taux de réussite : Une première idée était de faire trouver au système des chemins maximisant le succès aux exercices, (phéromones positives φ⁺) et minimisant les échecs (phéromones négatives φ^–). Le système s'est empressé de trouver des chemins optimaux qui, après analyse, étaient des raccourcis contenant le nombre minimal d'exercices simples permettant de valider le sujet. Le système créait même des arcs non prévus entre des items du début d'un sujet vers des items de fin du sujet, réalisant ainsi ce qui avait été demandé : trouver un chemin maximisant le succès. Ce résultat très encourageant quant au fonctionnement du système n'étant pas exactement celui souhaité par l'équipe pédagogique de Paraschool, un nouvel objectif a été fixé favorisant des chemins où l'élève moyen aurait un taux de réussite sur échec de 60/40, pour que les élèves soient confrontés à des exercices difficiles leur permettant de progresser, tout en leur laissant une impression de succès pour les motiver.
   
• Confrontation entre pédagogie et phéromones : Un second raffinement également testé est de réduire le poids pédagogique lorsqu'il y a suffisamment de passages de fourmis. Ainsi, le poids pédagogique est diminué proportionnellement à la quantité de phéromones présentes sur l'arc. Cela permet de confronter la pédagogie à l'ensemble des élèves. L'idée étant de trouver le délicat équilibre entre les deux parties afin de ne pas donner trop d'avantage à une partie (le système ne serait plus dynamique sinon). Au-delà d'un certain nombre de passages, le poids pédagogique n'a plus d'effet et l'adéquation au taux de réussite de 60 % reste le seul objectif à atteindre. Si par contre le passage des fourmis se réduit, le poids pédagogique reprend de l'importance. Cet effet peut être vu comme une force de rappel, qui aura tendance à revaloriser l'arc si la fréquentation diminue. Plus le poids pédagogique sera important, plus la force de rappel sera importante.

   Suivant les phéromones présentes sur l'arc, sa valeur (fitness) sera calculée de la façon suivante :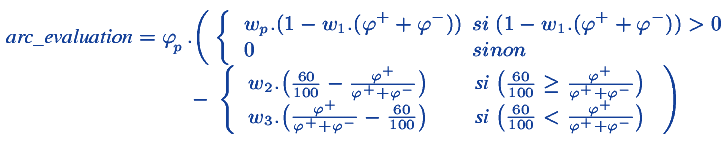

   La première partie reflète la confrontation entre la « pédagogie » (poids pédagogique ω_p) et la « collectivité » (quantité de phéromones φ⁺ + φ^–). Le poids ω₁ permet d'ajuster la quantité de phéromones au dessus de laquelle le poids ω_p n'aura plus d'influence.

   La deuxième partie de l'équation représente l'adéquation au taux de succès (objectif ici fixé à 60 %). Les poids ω₂ et ω₃ ont été dissociés afin d'avoir des pentes différentes au dessus et en dessous du taux de succès de 60 %, afin qu'il soit préférable de se trouver au dessus des 60 % qu'en dessous.

II.d. Sélection des arcs

   Lorsqu'un élève valide un item, il convient de choisir, parmi les arcs qui sortent de cet item, ceux qui seront proposés à l'élève. C'est le rôle de la procédure de sélection. C'est ici que sont utilisées les mesures de fitness. Une nouveauté par rapport aux algorithmes d'OCF est que la procédure de sélection est empruntée à l'évolution artificielle. En effet, les fourmis artificielles du paradigme OCF suivent le meilleur arc avec un bruit gaussien (elles se trompent de temps en temps). Dans notre algorithme, nous avons institutionnalisé cette composante stochastique en utilisant un vrai opérateur de sélection très bien étudié et documenté pour choisir l'arc à proposer. La procédure de sélection va choisir un arc de manière aléatoire mais biaisée par la mesure de fitness, permettant aux arcs « à fort potentiel » (avec une fitness élevée) d'être prédominants mais pas de manière déterministe. Il y aura de la place pour le hasard et l'exploration. Un bon opérateur de sélection doit permettre de régler la pression de sélection s. Plus s est grande, plus le meilleur arc a de chances d'être sélectionné. Des différentes façons d'écrire l'algorithme de sélection, la sélection par tournoi est probablement la meilleure : cette procédure très classique consiste à tirer s individus au hasard et de prendre le meilleur. Plus s est grand, plus le tournoi implique des arcs différents, et plus il est probable que l'arc qui l'emportera soit fort. Outre son efficacité algorithmique, cette méthode a l'avantage d'être très simplement paramétrable.

III. La notation ELO

   Dans ce souci d'individualisation de l'algorithme, le niveau des items doit être estimé pour éviter de proposer à l'étudiant un exercice bien trop facile ou bien trop difficile par rapport à son niveau. Mais comment évaluer réellement un exercice, et un élève ? La première idée est de demander aux professeurs qui créent un exercice d'en évaluer la difficulté sur une échelle allant de facile à difficile. Mais en plus d'être fastidieuse, cette méthode est, source d'erreurs, car l'évaluation de la difficulté dépend du jugement du professeur, sans tenir compte du niveau réel des élèves.

III.a Principe

   Une approche plus simple et plus efficace est d'avoir un système de notation automatique qui évalue la force des items, mais aussi des élèves. La solution sélectionnée est basée sur le système de notation Elo [Elo78], utilisé dans le monde des échecs depuis plus de 50 ans. Il surmonte les principales difficultés rencontrées par les systèmes de notation, sachant que :

• Les performances des joueurs changent au cours du temps en fonction de leur âge et de leur apprentissage.
• Elles peuvent même varier temporairement (à cause d'une maladie...).
• Le nombre d'entrées et de sorties de joueurs est assez important (chaque participant ne reste qu'un temps assez court dans la système).

   À la fin des années 50, en se basant sur le modèle de Thrusone et Case [BrTe52], le mathématicien A. E. Elo [Elo78] met en place un système de notation qui sera adopté par les fédérations mondiales d'échecs. Ce ne fut pas le premier système à être testé : Le premier fut crée en Allemagne par Hösslinger, suivant le system Ingo [Hos48]. Cependant le système Elo est plus efficace, du fait que la différence de niveau entre deux joueurs (S_i - S_j) est liée à la probabilité du joueur i de gagner contre le joueur j. De plus, le système Elo fut le premier à utiliser des ordinateurs pour ses calculs, permettant la notation d'un grand nombre de joueurs.

   L'équation

   L'influence de la différence R_ij - R_ije est réglée par le paramètre K, représentant la quantité maximum de points que deux joueurs peuvent s'échanger au cours d'un partie. Un coefficient K élevé donne plus d'importance aux résultats des parties récents, alors qu'un coefficient faible permet de plus tenir compte des performances ultérieures. Aux échecs, ce facteur K fluctue entre 16 pour les grands joueurs (score Elo > 2400) et 32 les plus faibles (score Elo < 2100).

   En suivant le modèle de Bradley et Terry [BrTe52], si la différence de niveau 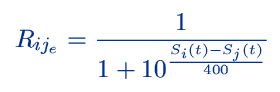S_i(t) - S_j(t) est connue entre deux joueurs, la probabilité de réussite du joueur i sur le joueur j est définie ainsi :

   C'est la formule de base qui est utilisée dans le système de notation de la fédération américaine d'échecs.

III.b. Inflation et Déflation des scores Elo

   Depuis l'introduction du système de notation Elo dans le monde des échecs, l'écart des scores continue à s'agrandir au fil du temps. Une des principales raisons est que les tournois d'échecs deviennent de plus en plus populaires et le système de notation Elo de plus en plus utilisé. Comme le nombre de joueurs ne cesse de croître, la probabilité d'avoir un joueur extrêmement fort ou faible augmente de plus en plus. Cette expansion de l'écart ne pose aucun souci au système Elo. Par contre, d'autres problèmes entrent en ligne de compte :

• Le nombre important de joueurs entrants et sortants, et
• l'influence de sous-groupes dans la notation.

   En créant une inflation ou une déflation générale dans le système de notation, ces facteurs mettent en cause « l'intégrité » du système Elo. Celle-ci est très importante, car elle permet de dire à quel point les scores calculés reflètent un niveau donné indépendamment du temps et parmi les différents sous-groupes de joueurs.

III.a.1. Entrées/Sorties

   Dans le système Elo en général, si aucun joueur n'entre ou ne sort, tout gain de points au cours d'une partie se répercute en une perte pour l'adversaire. Globalement les points sont conservés et la moyenne est maintenue au cours du temps. Mais il est clair que certains joueurs vont entrer dans le système de notation. Des scores provisoires et généralement bas vont leur être affectés. À l'inverse, ceux qui quittent le système sont plutôt bien notés du fait de leur expérience. Leur départ de bons joueurs, remplacés par des débutants va donc entraîner une « fuite » de points dans le système Elo. Cette diminution des scores est d'autant plus paradoxale que dans le même temps, le niveau des joueurs a tendance à augmenter... Les joueurs, qui se battent face à ces joueurs sous-évalués (mais en progression constante), ont alors tendance à obtenir des scores plus bas, ce qui entretient le cercle vicieux.

III.a.2. Existence de sous-groupes

   L'inflation ou la déflation ne se déroule pas uniquement sur l'ensemble des joueurs, mais aussi sur des sous-groupes. Un sous-groupe est un ensemble de joueurs isolés pendant de longues périodes sans contact extérieur. Les scores dans ce groupe peuvent dériver et être artificiellement bas ou haut. Au sein du groupe, les scores ont toujours une valeur prédictive, mais pas en dehors. La conséquence est qu'en jouant contre un joueur extérieur, le joueur verrait son score monter ou baisser très rapidement et, du coup, influencer le score de son compétiteur. L'intégrité de la notation en est directement affectée. Il est donc important pour les joueurs d'affronter périodiquement des adversaires n'appartenant pas à leur groupe habituel.

IV. Notation Elo dans le système de Paraschool

   Dans le système de Paraschool, nous allons considérer qu'élèves et items sont des adversaires qui se livrent un combat. Le système Elo peut donc être directement mis en application en utilisant les mêmes équations et paramètres que dans les tournois d'échecs, ce qui donnera un niveau ELO à l'élève, mais aussi à l'item.

   Une fois que le niveau d'un élève ou d'un item s'est stabilisé, les applications sont nombreuses :

• Les élèves peuvent connaître leur niveau et visualiser leur évolution.
• L'équipe pédagogique de Paraschool n'est plus obligée de mettre une note subjective sur chaque exercice.
• Le système Elo permet de détecter une possible erreur sémantique ou même pédagogique (difficile à trouver parmi plusieurs milliers d'exercices différents). En effet des valeurs extrêmes de Elo indiquent qu'il existe dans l'exercice soit une coquille, soit une erreur pédagogique (difficulté importante ou trop grande facilité). La notation Elo se révèle une aide précieuse pour l'équipe pédagogique de Paraschool.
• Pour finir (et c'était le but premier de cette implantation), ces informations peuvent être utilisées par l'hommilière pour éviter de proposé des items inadaptés à la force de l'élève.

IV.a. Entrées/Sorties

   Dans le cas de Paraschool, des élèves entrent et sortent du système en majorité en début et fin d'année scolaire. En théorie, une fois son compte créé, l'élève le conserve d'une année sur l'autre. Dans la pratique, les établissements remettent à jour leur liste d'élèves ainsi que leur comptes, entraînant chaque année, un nombre important d'entrées et de sorties.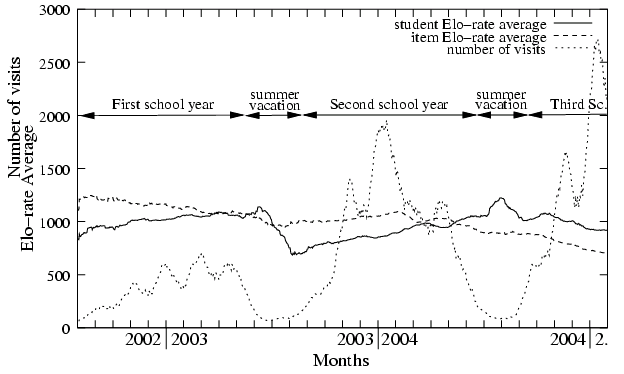

Figure 2 : Moyenne des notes Elo et nombre de passages sur une période de trois ans.

   Sur la figure 2, le nombre de passages indique clairement les périodes d'inactivités des grandes vacances scolaires. Entre deux, la moyenne du score Elo des élèves a tendance à augmenter, ce qui est plutôt un bon point (les élèves deviennent meilleurs). La brutale chute du niveau Elo des élèves pendant les vacances scolaires est une conséquence directe du nombre d'entrées et de sorties des élèves mais aussi du fait que chaque année, la société Paraschool gère de plus en plus d'élèves (de 50 000 à 200 000 élèves sur les trois ans).

   Le graphe 2 montre aussi que le niveau moyen Elo des items décroît années après années. À l'opposé des établissements, Paraschool ne réactualise pas ces items en début d'année scolaire. Ainsi comme les élèves deviennent de plus en plus forts, une déflation au niveau des scores des items se fait sentir de manière constante.

IV.a.2. Création de sous-groupes

   Dans le système de Paraschool, il existe deux cas de sous-groupes :

• Un item ne peut se mesurer à un autre item et il en va de même pour les élèves. Cela crée deux sous-groupes d'un autre type de ceux rencontrés aux échecs. En effet ces sous-groupes n'interagissent que par le biais de l'autre sous-groupe, rendant la dynamique assez différente.
   
• Le système de Paraschool révèle aussi d'autres sous-groupes avec l'existence des classes (CM1, 6^e, Terminale...). En effet les élèves d'une classe auront tendance à résoudre les exercices de leur niveau, un peu comme les joueurs d'échecs qui ne jouent qu'entre eux. La conséquence directe est l'impossibilité de pouvoir comparer les exercices venant de deux classes différentes.

   Une analyse plus précise est nécessaire pour mieux comprendre l'influence de ces sous-groupes.

IV.b. Difficulté globale sur Paraschool

   La figure 3 représente la différence de Elo entre l'élève et l'exercice en fonction des chemins empruntés par les élèves. La première phase est celle de stabilisation (L'hommilière tente de se stabiliser autour de l'objectif qu'on lui a fixé). Ensuite l'hommilière se stabilise autour d'une valeur de -200 Elo, signifiant qu'en moyenne les élèves se confrontent à des items ayant un score Elo de 200 points inférieurs à leur propre score. Ces 200 points représentent exactement une probabilité de réussite pour l'élève de 60 %. Ce résultat est une belle confirmation que l'hommilière réussit à globalement fabriquer des chemins sur lesquels les élèves ont une chance de réussir de 60 % (taux fixé par l'équipe pédagogique de Paraschool).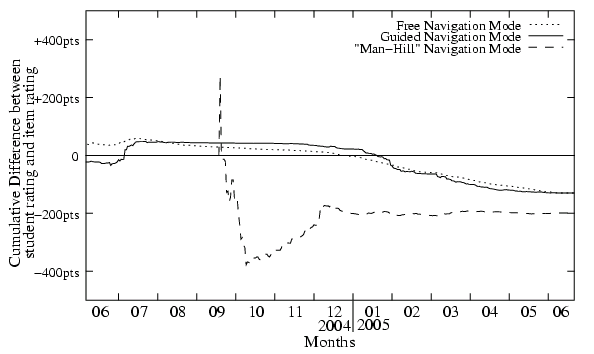

Figure 3 : Différence de score Elo entre l'élève et l'item
en fonction du type de navigation sur une période de un an.

Conclusion

   Cette tentative d'introduction d'intelligence dans la navigation du logiciel Paraschool a permis de montrer que les hommilières ne se comportent pas de la même manière que les fourmilières artificielles, que nous avons donc affaire à un nouveau paradigme se situant entre orientation d'utilisateurs sur un parcours et optimisation par colonie de fourmis. Le système semble stable, même s'il faut encore faire quelques analyses. Ce travail débouche donc sur l'étude comportementale des hommilières, dont la société Paraschool est un acteur essentiel. Les retombées en enseignement assisté par ordinateur semblent très importantes, car le modèle semble remarquablement bien adapté à cette tâche, mais de nombreuses autres applications semblent possibles dans d'autres domaines.

   En ce qui concerne la notation Elo, malgré ses imperfections connues, le système a prouvé sa stabilité au cours des tournois d'échecs de ces 50 dernières années. En ajoutant ce système automatique de notation au processus d'hommilière, Paraschool espère avoir une bonne idée du niveau des élèves et des items. Dans le même temps, l'équipe pédagogique obtient un retour de qualité sur le contenu et la pertinence des exercices. De leur côté, les étudiants pourront suivre leur courbe de progression relative (une valeur absolue n'ayant aucune signification pédagogique). Pour le moment, la notation Elo est calculée dans le système et a montré que le paradigme hommilière remplit les espérances de l'équipe pédagogique en suggérant des chemins au taux de réussite de 60 %.

   La prochaine étape sera d'indiquer aux élèves la force des exercices proposés. Par ce biais, le système pourra détecter le comportement des étudiants face à la difficulté. Par exemple, si un élève décide de se confronter à un exercice difficile, il sera classé comme élève combatif. À partir de là, l'hommilière pourra s'adapter à ce type d'élèves en augmentant la force des exercices proposés. À l'opposé, le niveau sera baissé si le système rencontre des élèves qui doivent être encouragés.

Bibliographie

[BaBe79] Batchelder W. H., Bershad N. J. (1979). The Statistical Analysis of a Thurstonian Model for Rating Chess Players, in Journal of Mathematical Psychology, 19, 39-60.

[BDT99] Bonabeau E., Dorigo M., Theraulaz G. (1999). Swarm Intelligence : From natural to Artificial systems, Oxford University Press, ISBN 0-19-513159-2.

[BDT00] Bonabeau E., Dorigo M. & Theraulaz G. (2000). Inspiration for optimization from social insect behaviour, in Nature, vol. 406, p. 39-42.

[BrTe52] Bradley R. A., Terry M. E. (1952). The Rank Analysis of Incomplete Block Designs, The Method of Paired Comparisons, Biometrika, 39, 324-345.

[CDM91] Colorni A., Dorigo M. & in proceedings of European Conference on Artificial Life, Cambridge, MIT Press, p. 134-142.

[DAG+90] Deneubourg J.-L., Aron S., Goss S. & Pasteels J.-M. (1990). The self-organizing exploratory pattern of the argentine ant, in Journal of Insect Behaviour, vol. 3, p. 159-168.

[DBT00] Dorigo M., Bonabeau E. & Theraulaz G. (2000). Ant algorithms and stigmergy, in Future Generation Computer Systems, vol. 16, p. 851-871.

[DePa83] Deneubourg J.-L., Pasteels J.-M. et Verhaeghe J.-C. (1983). Probabilistic Behaviour in Ants: a Strategy of Errors ?, Journal of Theoretical Biology, 105.

[DoDi97] Dorigo M. & Di Caro G. (1997). The ant colony optimization metaheuristic, in D. Corne, M. Dorigo and F. Glover (Eds), New ideas in optimization, McGraw-Hill, p. 11-32.

[Dor92] Dorigo M. (1992). Optimization, learning and natural algorithms, PhD Thesis, politecnico di Milano.

[DPV83] Deneubourg J.-L., Pasteels J.-M. & Verhaeghe J.-C. (1983). Probalistic behaviour in ants : a strategy of errors?, in Theoretical Biology, vol. 105, p. 259-271.

[Elo78] Elo A. E. (1978). The rating of chess players past and present, New York: Arco Publishing.

[GoDe91] Goldberg D. E. & Deb K. (1991). A comparative analysis of selection schemes used in genetic algorithms, in G. Rawlins, editor, Foundations of Genetic Algorithms, vol. 1, p. 69-93.

[Gol89] Goldberg D. E. (1989) Genetic algorithms in search, optimization and machine learning, Addison-Wesley Publishing Company Inc., Reading, MA.

[Hos48] Hösslinger A. (1948). Ingo System, Bayerischen Schachnachrichten. (From [Elo78]).

[LMV02] Labroche N., Monmarché N. & Venturini G. (2002). A new clustering algorithm based on the chemical recognition system of ants, in proceedings of the European Conference on Artificial Intelligence, IOS Press, p. 345-349.

[LMV03] Labroche N., Monmarché N., Venturini, G. (2003). AntClust: Ant Clustering and Web Usage Mining, Genetic and Evolutionary Computation Conference, Erik Cantu-Paz (Eds.). Lecture Notes in Computer Science 2723 Springer-Verlag Telos. Chigago, july 12-16. p. 25-36.

[Mer97] GRIMPS (1997). Great Internet Mersenne Prime Search, 2^2976221-1 is now the Largest Known Prime, GIMPS Discovers 36th Known Mersenne Prime. Press Release, Sept. 1997.
http://www.mersenne.org/2976221.htm.

[Res94] Resnick M. (1994). Turtles, termites and traffic jams : Explorations in massively parallel microworlds, Complex adaptive systems series MIT Press.

[SeCo03] Semet Y., Collet P. (2003). Application de l'optimisation par colonies de fourmis à la structuration automatique de parcours pédagogiques, Revue EPI.
www.epi.asso.fr/revue/articles/a0309b.htm.

[SJB03] Semet Y., Jamont Y., Biojout R., Lutton E. & Collet P. (2003). Artificial Ant Colony and E-Learning : An optimization of pedagogical paths, HCII 2003.
Télécharger ce texte au format PDF (56 Ko)

[SLC03] Semet Y., Lutton E. & Collet P. (2003). Ant Colony Optimisation for E-Learning : Observing the emergence of pedagogic suggestions, SIS 2003.
Télécharger ce texte au format PDF (123 Ko)

[StDo99] Stützle T., Dorigo M. (1999). ACO Algorithms for the travelling salesman problem, in M. Maleka, K. Miettinen, P. Neittaanmaki, J. Periaux (Eds), proceedings of the EUROGEN conference, John Wiley & Sons, p. 163-183.

[VJB05] Valigiani G., Jamont Y., Biojout R., Lutton E., Collet P., Experimenting with a Real-Size Man-Hill to Optimise Pedagogical Paths, in H. Haddad et al. Eds., Symposium on Applied Computing (SAC), ACM, Santa Fe, New Mexico.

Notes

Note 1 : Un exemple équivalent touche les travaux de classification de sessions web par des fourmis. Chaque session est associée à une fourmi et le nombre de visites peut être important [LMV03].

Note 2 : Informations déposées sur les arcs non permanentes.

___________________
Association EPI
Mars 2006