Béquilles pédagogiques pour logo en CP et CE1
Un matériel en carton
D. Bertin
Nous reproduisons ici un article du Dossier EPI n° 6, Informatique à l'école, (supplément au Bulletin de septembre 1984), p. 75-89. Le préambule de ce dossier « Éléments d'Histoire », déjà en ligne à http://www.epi.asso.fr/revue/dossiers/d06p005.htm, comprend un tableau faisant état des diverses composantes que l'on pouvait envisager – il y a trente ans – pour les activités relatives à l'informatique dans le cadre de l'école élémentaire. Les trois premières parties réfèrent explicitement aux trois paragraphes de la circulaire ministérielle de mars 1984.
Introduction
Cet article présente sommairement un jeu de pièces en carton que j'ai été amené à développer dans le cadre d'une recherche INRP.
Ce matériel répond au cahier des charges suivant :
- simplicité de fabrication,
- simplicité de mise en oeuvre dans une conduite de classe même « traditionnelle » (mais avec respect des démarches de chaque enfant),
- niveau CP/CE1.
Pour rester concis, je décrirai ici des pistes exploitables, sans les attendus théoriques ou psychopédagogiques qui sous-tendent le travail avec ce matériel. Le lecteur curieux pourra se reporter pour plus de détails au rapport complet dont les passages ci-dessous sont extraits.
Toutes les situations ici proposées ont été testées à l'École Dunoyer de Segonzac (Antony) dans la classe de Bernard Henry (CP en 83, CE1 en 84).
Par commodité, j'appellerai LOGO-CARTON l'ensemble des pièces en carton et les manipulations qu'elles supportent, LOGO-MOBILE le Promobile Jeulin, système autonome et programmable par cartes. LOGO-MICRO désignera la donnée d'un micro-ordinateur parlant LOGO, que celui-ci pilote une « tortue » graphique ou un promobile au sol.
1ère partie : Le jeu de pièces LOGO-CARTON
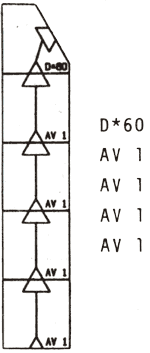
La figure 1 présente l'ensemble des cartons utilisables par les enfants.
Ces pièces sont réalisées dans un fort bristol, glacé sur sa face visible, peluché (anti-glisse) sur la face support. Les cotes minimales sont de 4 cm au niveau des bases. On repérera sur ces pièces, accroché à l'une des arêtes, un triangle équilatéral, et en complément, sur une autre arête, une embase elle aussi équilatère. Bien entendu, au contact de deux pièces, on recompose un triangle équilatère.
Embase et pointe sont reliées par un trait, en sorte que faire abouter des cartons peut être interprété comme la construction de chemins à sens unique, ou l'histoire d'une petite « tortue », c'est à dire les différents stades de son déplacement. Enfin, on peut lire des codes plus ou moins inspirés des primitives graphiques LOGO, une mnémonique AV, D*, G* suivie d'un nombre entier.
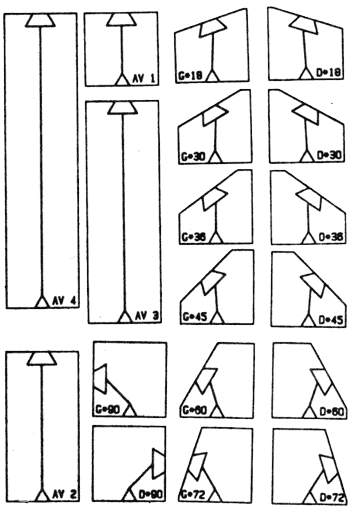
Figure 1.
Si les pièces AV n renvoient directement à leurs homologues informatiques, il n'en va pas de même des pièces coudées qui prennent en charge du mouvement, selon des directions relatives, parfois étranges, et du tournant. Toute pose produit donc un résultat sensible en cap et en position ; à une simulation (pseudo-)continue dans la géométrie Tortue, LOGO-CARTON oppose une simulation discrète faite de quantums de déplacements, de déplacements-tournés. L'astérisque du codage marque cette différence. Au demeurant, la géométrie ainsi induite est plutôt naturelle : un avion, une automobile, un tricycle, un piéton etc. tournent en avançant.
Maintenant, place à la pratique.
2ème partie : Premières manipulations
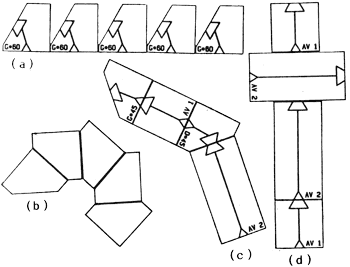
[M1] pour une première prise de contact, on distribue aux enfants un petit lot de pièces qu'il s'agit de décrire, éventuellement de classer. Puis on proposera de mettre « bout-à-bout » quelques éléments de jeu. La figure 2 présente quelques réalisations (niveau CP) et le titre que leurs auteurs leurs ont attribués.
|
|
(a) « des voitures qu'on accroche »
(b) « un serpent enroulé » ou « une trompe »
(c) « un chemin »
(d) « une statue »
Figure 2. |
[M2] On peut alors soulever le problème des raccords en se lançant dans une recherche extensive de toutes les façons d'abouter 2 pièces. A cet endroit, il peut être utile de disposer d'exemples plus grands pour affichage au tableau.
Les enfants trouveront vite une typologie des (presque) bonnes formes d'accrochage :
|
« en triangle »
|

« en losange »
|
« en noeud papillon »
|
Figure 3.
D'où sortira enfin la règle :
Romaric : « on prend le triangle parce que ça fait des flèches, et les flèches ça fait des chemins. »
Virginie : « on dirait que ça fait une route avec des flèches par terre (ce point est décisif pour la suite des opérations : dès qu'il y a accord sur la règle d'aboutage au sein du groupe-classe, il y a acceptation de l'idée de constituer des chemins, monosens, c'est-à-dire avec un début, un sens de parcours et une fin. Cette règle doit fonctionner ; aussi on distribue des cartons supplémentaires aux enfants, avec consigne de fabriquer de tels chemins). »
[M3] dans Ml et M2, seuls des critères topologiques ont pu intervenir dans la manipulation des pièces : ce qui donne de l'unité dans la production des assemblages, c'est l'absence de solution de continuité des graphismes obtenus. D'une certaine façon, les codages ont pu ne jouer aucun rôle, bien qu'implicitement présents dans l'idée de chemin. Rien de tel, pour passer à l'explicite, qu'un jeu-du-télégramme.
Figure 4.
À cet effet, on proposera à chaque enfant de :
- construire un chemin,
- décrire sur une feuille de papier le chemin,
- passer à son voisin le message ainsi obtenu,
- reconstituer le chemin du voisin à réception de son message,
- comparer les deux chemins produits, avant émission, après réception.
En CP, cet exercice peut se révéler redoutable. Voici un exemple de difficulté pouvant surgir : l'ambiguïté du codage.
Il est rare qu'au premier jet, les télégrammes soient correctement écrits : sans parler des problèmes de calligraphie, ceux-ci sont très souvent spatialisés. La figure 4 en donne un exemple typique : le chemin a manifestement été construit en fuite par Virginie, qui pense son chemin comme celui qu'elle emprunterait, donc devant s'éloigner d'elle. Le problème, c'est qu'à la relecture, son voisin lira de haut en bas, produisant un chemin différent, d'où conflit. Comme souvent en pareil cas, ce conflit est riche pédagogiquement parlant. Il s'agit de déboucher sur l'isomorphisme :
parcours ordonné du chemin LOGO-CARTON
↔
parcours ordonné et linéaire du texte écrit.
[M4] Maintenant, on s'occupe des angles et plus particulièrement du fameux théorème du trajet total de la tortue qui indique que la variation totale du cap de la tortue décrivant un circuit fermé est un multiple – positif ou négatif – de 360°. Bien entendu il est hors de question d'atteindre ce théorème qui suppose, en particulier, une bonne maîtrise de la notion d'angle. Ici, il ne peut s'agir que d'une approche, pour plus tard.
En résumé, on demande aux enfants de construire des chemins fermés et réguliers. Comme ces deux adjectifs sont lourds de sens, on travaille à la fois sur le plan du linguistique et du géométrique. La figure 5 donne des exemples de construction dont les pièces AV n ont été bannies.
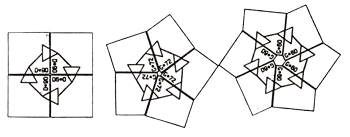
Figure 5.
Découle de cette phase une nomenclature :
|
Nombre de pièces identiques nécessaires |
Code de la pièce |
Message LOGO-CARTON |
|
|
|
|
La forme même des messages, surtout s'ils sont longs, appelle « naturellement » l'introduction du primitif REPETE. D'ailleurs, Pierre : « c'est régulier parce qu'on répète toujours pareil - on répète qu'on tourne pareil. »
À l'issue de cette phase, on gagne les acquis suivants :
- un catalogue de formes régulières et d'angles associés à 4, 5, 6... côtés,
- un début de définition,
- plus tourné vers le Code, le premier exemple de dissolution d'une suite d'ordres dans une totalité de rang conceptuel plus élevé, juste avant la notion de procédure.
On peut (on doit) tester l'effet de ces suites d'instructions sous LOGO-MICRO en tapant REPETE <val> [TD ou TG angle] ou sous LOGO-MOBILE en répétant <val> fois l'insertion dans le lecteur de cartes de la même carte de pivotement.
Et là, surprise! la tortue tourne sur place, laissant évidemment comme seule trace un point. Il y a rupture entre la géométrie supportée par LOGO-CARTON et celle induite par LOGO. D'où un travail sur la vraie nature des changements d'état de la tortue et le tracé des polyèdres réguliers.
Christophe : « si on veut faire avec Choupette comme en carton, il faut rajouter des AVANCE. » (Choupette est le patronyme donné au promobile par les enfants de B. Henry.)
Par ailleurs, on gagne le 360° en faisant rechercher par quelle commande (unique) on peut obtenir de la tortue un tour complet, (attention, les deux cartes correspondantes n'existent pas sur le système JEULIN : les fabriquer.) Par un aller-retour nomenclature/formes régulières sous LOGO-CARTON vs manipulations LOGO-MOBILE (ou MICRO), on atteint le mini-théorème : (nombre de fois qu'il faut répéter) par (angle dont on tourne) = 360°.
(bien entendu, la question de l'angle et de sa mesure n'est pas réglée ; modestement, on a fourni quelques images mentales pour l'avenir et opérationnelles pour l'immédiat. Cette induction pédagogique n'est pas pire que les autres).
3ème partie : LOGO-CARTON et anticipation
Dans les activités suggérées ci-dessus, l'aspect puzzle risque de prédominer puisque la réalisation d'une consigne ne passe pas nécessairement par un ordre programmatique - au sens d'une énonciation linéaire ordonnée des « commandes » – avant réalisation (comme en LOGO). L'ordre peut venir après, c'est ce que j'ai appelé re-parcours.
Pour le dire autrement, la réalisation d'une figure sous LOGO passe par la mise au point d'une suite réglée de changements d'état de la tortue : d'un état initial, celle ci passe par une série d'états intermédiaires pour aboutir à un état final en sorte que la trace de cette dynamique est le motif désiré. En revanche, sous LOGO-CARTON, le dessin final n'est relié qu'après coup à la série d'états intermédiaires (c'est-à-dire tels qu'on peut les lire sur le codage déroulé) : les pièces peuvent être posées dans un ordre autre que celui du codage final. Aussi, on peut toujours employer un vocabulaire fortement connoté par la notion de déplacement, de chemin, de route, etc. Rien n'empêchera l'enfant de penser-puzzle. Comme j'espère l'avoir montré en M4 ce peut être une bonne chose ; mais si on veut induire une pensée plus proche de LOGO, il faut introduire un matériel qui fixe des états de départ et d'arrivée. Ce matériel a été :
Un grand terrain de jeu pour LOGO-CARTON
Comme le montre la figure 6, il s'agit d'un quadrillage de 6 par 9 cases de 4 cm. de côté chacune. Évidemment, on ne pourra plus poser que des pièces droites ou « à angle droit ». Sur le pourtour, j'ai dessiné des pointes ou embases de triangles équilatéraux alternées. On notera la particularité des coins, deux d'entre eux seulement pouvant accueillir un G*90.
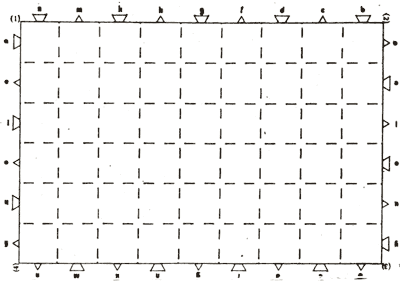
Figure 6.
Ce terrain de jeu sera le lieu de pratiques LOGO-CARTON par essence locales (vers la Forme, intrinsèque). Par opposition, existent des repères globaux, voyelles pour une direction, consonnes pour l'autre, permettant de désigner sans ambiguïté toutes les cases ; ces lettres sont disposées selon deux systèmes symétriques sous un demi-tour, afin de ne pas privilégier une présentation de la feuille particulière.
[S1] Longueur ? structure additive et classement
En CP, on se contentera de travailler avec des chemins droits, en cherchant tous les chemins joignant un bord à son opposé. On retrouve une situation classique, que l'on pourra travailler sous toutes les coutures : plutôt tournée vers la construction effective de chemins, avec transfert sous LOGO-MICRO ou MOBILE ; plutôt tournée vers un travail sur les écritures, messages à trous etc. Par ailleurs, on pourra en profiter pour introduire le primitif REPETE, à l'occasion par exemple de jeux par équipes avec LOGO-MICRO type « course-à-n ».
En CE1, on sera plus exigeant en cherchant sur tous les chemins, qu'ils soient droits ou possèdent un tournant. Voici une série de questions :
Quels sont les chemins les plus courts possibles ? Donner les cases occupées. Quels sont ceux juste après ? Peut-on les dénombrer ? Quels sont les chemins droits les plus courts possibles ? Donner des exemples. Comment décrire les cases occupées ? Peut-on prévoir le nombre total de ces chemins droits les plus courts ? Mêmes questions, mais avec les chemins droits les plus longs. Si on veut construire des chemins plus courts que les chemins droits les plus longs, mais plus longs que les chemins droits les plus courts, comment s'y prendre ? Si on appelle longueur d'un chemin droit ou tournant une fois le nombre de cases occupées, minimum ? Maximum ? Pour tout nombre compris entre ces deux extrêmes, y a-t-il un chemin, dont ce nombre est la longueur ?
Ces questions pourront sembler « bateaux » ; pourtant, il s'agit de réelles situations-problèmes pour des CE1. Des solutions, mathématiques, consisteraient à se retourner vers le code pour qu'il prenne en charge les situations. Bien évidemment de telles mises-en-équation sont impossibles ici, en sorte que les enfants devront mettre en place des stratégies de gestion de l'information, soit sous forme de tableaux, soit sous forme de marques graphiques – organisées – sur des réductions du terrain de jeu.
[S2] TTTT et quarts de tour
Ici, on va s'intéresser aux chemins qui tournent et plus particulièrement au nombre de D*90 ou G*90 mis en jeu.
Donc on fait construire des chemins d'un bord à l'autre, en autorisant le chevauchement des cartons. Voici une série de questions à poser aux enfants :
- peut-on aller de n'importe quel bord à n'importe quel bord ? Donner des exemples en précisant :
- la case de départ,
- la case d ' arrivée,
- le nombre de pièces-qui-tournent et leur nature.
- même type de questions mais en ajoutant une contrainte sur les bords :
- d'un bord au bord opposé,
- d'un bord à ce même bord,
- d'un bord à un bord adjacent.
On veut donc faire verbaliser (à défaut vivre) la règle suivante :
- soient Bl et B2 deux bords.
- si Bl et B2 sont opposés, le nombre cherché est pair, et il y a autant de D*90 que de G*90
- si Bl et B2 sont confondus, alors ce nombre est encore pair, mais la répartition D*90/G*90 marque un déficit de deux unités pour l'une des deux classes.
- si Bl et B2 sont adjacents, alors le nombre de pièces qui tournent est impair.
Il s'ensuit que pour aller d'un bord à son opposé avec un chemin dont les piëces-qui-tournent sont toutes de la même classe, alors il faut utiliser 0, 4, 8, etc. ; telles pièces ; etc.
Bien entendu, on consolide ce frais savoir grâce au promobile que l'on fait piloter sur une reproduction à l'échelle du terrain de jeu.
[S3] Parcours, obstacles et anticipation
Jeu n° 1 (individuel )
Sur le terrain de jeu on dispose quelques obstacles ; on demande le chemin minimal qui permette de joindre une position de départ à une arrivée (via le codage LOGO-CARTON). Inversement, on présente un message, et on demande de trouver les obstacles qu'il aurait fallu distribuer sur le terrain de jeu pour que ce message soit celui d'un chemin minimal.
Jeu n° 2 (deux joueurs)
Pièces autorisées : AV 1, AV 2, AV 3, AV 4, D*90, G*90.
Position de départ : case (g,a).
Principe : chaque joueur pose à son tour une pièce sur le terrain en continuation du chemin déjà entrepris.
Perd celui des deux joueurs qui ne peut plus jouer parce que :
- l'autre joueur a atteint la rive opposée (avec bon accrochage de sa pièce gagnante).
ou
- il ne lui est plus possible de poser de pièce sans cogner dans un bord (autre que la rive salvatrice, ou bien avec mauvais accrochage sur celle-ci), ou dans le chemin déjà constitué.
La figure 7, ci-dessous, présente une partie entre deux enfants. Pour plus de clarté, j'ai marqué de noir les pièces posées par le premier joueur. Celui-ci gagne grâce à la pose en (u,m) d'un G*90 .
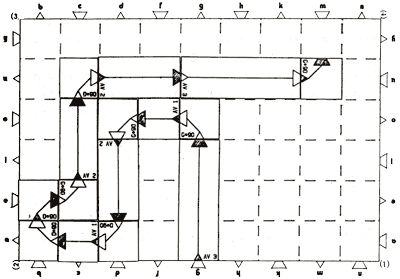
Figure 7.
[S4] Anticipation et conduite de processus
Le jeu du cariste
La figure 8 décrit le terrain d'évolution du promobile.
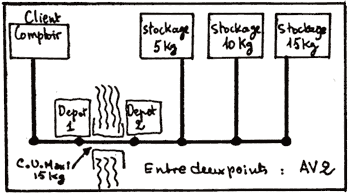
Figure 8.
Le problème posé aux enfants est le suivant :
le promobile est initialement face au comptoir (les enfants traduisent face à sa maison). il s'agit de piloter le promobile pour qu'il rapporte à ce comptoir un paquet de 5 kg, un paquet de 10 kg et un paquet de 15 kg.
Évidemment, il y a des contraintes qui sont :
sur le parcours se trouve un pont qui supporte une charge utile maximale de 15 kg (ouverture : que lit-on sur les plaques des camions, sur les panneaux de bord de routes ?). le promobile doit accomplir sa tâche en faisant le minimum de chemin, Par ailleurs, le pilotage doit appeler le minimum de cartes, cartes procédure comprises.
Cette situation est la plus riche de toutes celles présentées dans ce papier. On ne ratera pas l'occasion avec les enfants de leur faire construire la maquette où évoluera le promobile, de faire des dessins de celle-ci, d'y tracer éventuellement les cheminements voulus, enfin de rédiger des esquisses de solution du problème.
Un dernier point avant de conclure : comment le promobile peut-il être transformé en cariste ? Voici la solution imaginée par les enfants de B. Henry :
On installe un plateau sur le porte-crayon et un « chapeau » sur la coque. De la sorte, le promobile n'a le droit de rouler que le plateau levé. Les enfants ont rajouté une symbolique supplémentaire : arrivé quelque part, le promobile sonne pour indiquer qu'une manipulation sur des paquets doit avoir lieu ; s'il s'agit de charger un paquet, les yeux s'allument, et clignotent s'il s'agit d'en déposer un. Enfin, les yeux sont éteints pendant le transport.
Conclusion
Ce qui caractérise le travail suggéré ci-dessus, c'est in fine la double écriture-lecture suivante :
|
Écriture d'un codage sous LOGO-CARTON |
↔ |
effet produit, forme construite |
|
|
transcodage |
|
|
analyse des caractéristiques communes, recherche des invariants, des différences |
|
Écriture d'un codage sous LOGO-MOBILE/MICRO |
↔ |
effet produit |
|
On met donc en place une stratégie d'acquisition de quelques concepts LOGO à base de transferts directs (reconnaissance d'analogies pertinentes donc de formes stables) d'une part, de ruptures entre les modèles (conflits au niveau des effets attendus d'un même message) d'autre part.
Si on s'intéresse au géométrique, LOGO-CARTON facilite la linéarisation des formes de base avant passage à la programmation. Si en revanche, on se tourne vers la conduite de projet comme en S4, alors on offre à l'enfant un exemple typique d'enrichissement d'une situation algébrique.
D. Bertin
Cet article est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification) <http://creativecommons.org/licenses/by-nd/2.0/fr/>.
Bibliographie
Le Monde de M. C. Escher ou La vie et l'oeuvre de M. C. Escher (Chêne-Hachette). Les deux xylogravures « Tourbillons » et « Reptiles » montrent des animaux stylisée à la queu-leu-leu . Il « agit dans » chaque cas d'un seul animal dont on voit des états successifs. Comme en LOGO l'oeuvre escherienne met à plat la circulation d'une « tortue » ; l'étude en classe de telle oeuvres me semble vivement conseillée.
Ermel, Apprentissages mathématiques à l'école élémentaire, (Sermap-Hatier).On lira plus particulièrement l'introduction du tome dédié au CP (initiation au langage mathématique) et les pages 6 à 12 du CE (tome 1). S'agissant de ta géométrie, on se reportera au chapitre 4 du même tome, Consulter aussi L. Lurçat, L'enfant et l'Espace » (PUF, 1976).
Jacques Bertin, « La Graphique » in Communications n° 15, Seuil, 1970. Aussi Sémiologie Graphique (Gauthier-Villars) et « Voir ou lire » in Cartes et figures de la Terre (Centre Pompidou). Ce dernier ouvrage offre une multitude d'approches sur le problème de l'espace et sa prise en charge par des codes tout à fait passionnant pour le pédagogue.
Roberto Gimeno, Apprendre par la Graphique (Retz, 1980).Exemples à l'appui, l'auteur montre comment la graphique peut servir une démanche active qui aide à construire à partir d'une forme visuelle, ta pensée logique de l'entant. L'entant est ainsi amené à expérimenter spontanément sur le code et le méta-code. Cet aspect ,rejoint une problématique LOGO.
François Boule, Mathématique et jeux, (CEDIC,1976). On se reportera au chapitre 6 pour établir le lien avec LOGO-CARTON. On peut aussi consulter la publication n° 44 de l'APMEP, Jeux 1, et plus particulièrement l'article de Francis Gutmacher « Jeux d'un bord à l'autre ».
|