|
Tout a un reflet numérique
Jean-Pierre Archambault
Qu'est-ce que l'information ? Comment la représenter, la manipuler ? À chaque instant, notre cerveau capte, enregistre, et traite des informations. Ainsi pouvons-nous regarder, mémoriser, analyser, puis retranscrire une image, un texte ou un son. Depuis longtemps, l'homme a cherché à capter et reproduire ce reflet de la réalité par un dispositif technique. Et il a inventé le téléphone, la photographie, le cinéma... Mais qu'en est-il aujourd'hui, avec les machines que nous utilisons, qui sont des dispositifs de calcul programmé ?
Fabriquer un reflet numérique d'un objet réel
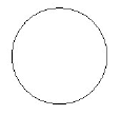 Comment introduit-on l'information dans une machine ? Comment la code-t-on pour pouvoir ensuite la manipuler ? Nous allons illustrer les principes de codage avec celui d'un dessin simple, décrit par une définition structurée. Comment faire pour décrire un dessin ? Par exemple, comment décrire le dessin ci-contre (figure 1) ? Comment introduit-on l'information dans une machine ? Comment la code-t-on pour pouvoir ensuite la manipuler ? Nous allons illustrer les principes de codage avec celui d'un dessin simple, décrit par une définition structurée. Comment faire pour décrire un dessin ? Par exemple, comment décrire le dessin ci-contre (figure 1) ?
Une solution est de dire : « Cette image est formée d'un cercle ». Nous pouvons même être plus précis et indiquer les coordonnées du centre du cercle, son rayon, sa couleur, l'épaisseur du trait... À partir de cette description, n'importe qui pourrait reconstituer le dessin.
 Cette méthode marche bien pour ce dessin-ci. Mais tout décrire avec des mots serait bien moins pratique pour le dessin ci-contre (figure 2) : Cette méthode marche bien pour ce dessin-ci. Mais tout décrire avec des mots serait bien moins pratique pour le dessin ci-contre (figure 2) :
En effet, comment facilement décrire en détail ces traits qui semblent tracés au hasard ? Qu'en serait-il avec un dessin qui représente un objet réel, ou un visage ?
Décrire avec des nombres binaires
Une autre méthode, qui a l'avantage de pouvoir être utilisée pour n'importe quel dessin, consiste à superposer un quadrillage au tracé (figure 3).
Chacune des cases de ce quadrillage s'appelle un pixel (contraction de picture element, en anglais). On noircit ensuite les pixels qui contiennent une portion de trait (figure 4).
Puis, il nous suffit d'indiquer la couleur de chacun des pixels, en les lisant de gauche à droite et de haut en bas, comme un texte (dans notre culture occidentale). Ici, cela donne : blanc, noir, noir, noir, blanc, noir, noir, blanc, noir, noir, noir, blanc, blanc, blanc, noir, noir, noir, blanc, noir, noir, blanc, noir, noir, noir, blanc.
De fait, cette description est assez approximative, et on constate une grande différence entre ces deux images :
Mais nous pouvons rendre la description plus précise en utilisant un quadrillage, non plus de cinq x cinq, mais de cent x cent pixels.
Et à partir de quelques millions de pixels, nous ne serions plus capables de faire la différence entre les deux images. Cette méthode est donc approximative, mais universelle : n'importe quel dessin, même très compliqué, se décrit exactement comme un dessin simple.
Ce dessin se décrit donc par une suite de mots « blanc » ou « noir ». Comme seuls les mots « noir » ou « blanc » sont utilisés, nous pouvons être plus économes et remplacer chacun de ces mots par un seul symbole, par exemple le mot « noir » par la lettre « n » ou le chiffre « 0 » et le mot « blanc » par la lettre « b » ou le chiffre « 1 ». Le dessin ci-dessus, avec une grille de 5 x 5, se décrit alors par la suite de 25 chiffres : 1000100100011100010010001.
Décrire numériquement toutes sortes d'objets
Le point clé consiste à convenir d'un standard pour toutes et tous. Il faut que tous soient d'accord pour décrire tous les dessins de la même façon. Décider, comme fait dans notre exemple, que le noir est représenté par 0 et le blanc par 1 et que les pixels se lisent de gauche à droite et de haut en bas. Il faut se mettre d'accord sur un standard. Le codage de l'information est avant tout une affaire de... convention. La méthode peut aussi être appliquée à une photo, un texte, un son, des nombres (entiers ou réels) : on peut convenir d'un codage pour toutes les informations !
Il faut distinguer comment coder l'information selon qu'elle est discrète, c'est-à-dire qu'on peut la dénombrer (par exemple, les lettres d'un alphabet), ou continue, auquel cas on doit sélectionner un nombre fini d'échantillons qui la représentent et à partir desquels il est possible de reconstruire une approximation du signal original (par exemple, un son).
Pour en savoir plus sur ces codages (des codages binaires), sur la notion d'information, qui en particulier se mesure, comme d'autres quantités (son unité est le bit, l'atome d'information est le bit 1 ou 0, deux informations non redondantes s'ajoutent, etc.) reportez-vous à l'article « Tout a un reflet numérique », paru dans la revue Interstices, dont ce texte est un extrait .
http://interstices.info/jcms/c_43823/tout-a-un-reflet-numerique
sur http://interstices.info/jcms/jalios_5127/accueil1
Jean-Pierre Archambault,
président de l'association Enseignement public & informatique
Paru dans une plaquette « Un enseignement au numérique dans notre académie » adressée à tous les enseignants de l'académie de Clermont-Ferrand.
http://www.epi.asso.fr/revue/artic/a1310d_enseignement_numerique.pdf
Cette contribution est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification) <http://creativecommons.org/licenses/by-nd/2.0/fr/>.
|