|
Impact de l'apprentissage par problème
sur la compréhension conceptuelle
de la mécanique newtonienne
Mohamed Droui, Abdelkrim El Hajjami,
Mohamed Bouklah, Salaheddine Zouirech
Résumé
Dans cet article, nous tentons d'explorer l'impact de l'apprentissage par problème, en utilisant des technologies de l'information et des communications, sur la compréhension conceptuelle de la mécanique newtonienne. Cent quatre vingt-dix élèves marocains au secondaire qualifiant (90 élèves du groupe expérimental et 90 élèves du groupe témoin) ont participé à cette étude. Nous avons utilisé l'inventaire du concept de force (FCI) pour mesurer La compréhension conceptuelle de la physique newtonienne. Le test FCI est un test conceptuel composé de 30 questions à choix multiples. Chaque mauvais choix pour chaque question correspond à une conception naïve spécifique sur les concepts de la force et du mouvement. Les données issues de cette étude sont analysées en utilisant les statistiques descriptives et le test t pour les comparaisons les données des deux groupes témoin et expérimental. Cette étude nous a montré que les élèves du groupe expérimental ont obtenu des résultats meilleurs que ceux du groupe témoin. La différence entre les gains normalisés d'apprentissage des deux groupes est statistiquement très significative. Les résultats de la présente recherche rapportent des effets positifs de l'apprentissage par problème centré sur les besoins des apprenants et qui intègrent les technologies au bon moment et pour la bonne activité.
Mots clé : Apprentissage par problème (APP), Expérimentation assistée par ordinateur (ExAO), Simulation, l'inventaire du concept de force (FCI).
Introduction
En science de l'éducation, des recherches ont fréquemment rapporté que l'approche traditionnelle de l'enseignement en sciences physiques ne parvient pas à aider les élèves pour développer une compréhension conceptuelle des concepts les plus fondamentaux (Pundak et Rozner 2008, Redish et al. 1998 ; Mazur, 1997). L'apprentissage par problème (APP) se présente aux enseignants de la physique comme une alternative innovatrice pour pallier à cette situation. En effet, de nombreuses études ont marqué des effets positifs de la mise en oeuvre de cette approche, particulièrement en médecine et en ingénierie, sur la motivation des élèves, sur le développement des compétences de travail en groupe, de recherche d'information et de communication ainsi sur l'acquisition de connaissances de base (Raine et Collett, 2003 ; Neild, 2004). Dans cet article, nous tentons d'explorer l'impact d'un scénario d'apprentissage par problème en utilisant une simulation et une expérimentation assistée par ordinateur (ExAO) sur la compréhension conceptuelle de la physique newtonienne.
1. Apprentissage par problème
1.1. Bref historique
En 1897, John Dewey déclarait : « Education, therefore, is a process of living and not a preparation for future living ». En considérant que l'enseignement de la médecine est un « processus de vie », les professeurs de la faculté de médecine de l'Université McMaster développèrent l'apprentissage par problème (APP) en 1969 (Albanese et Mitchell, 1993 ; Vernon et Blake, 1993). Ils présentèrent à leurs élèves des problèmes cliniques qui ne pouvaient être résolus qu'en acquérant les connaissances médicales pertinentes. L'APP s'avéra efficace et plusieurs autres écoles de médecine adoptèrent l'approche, y compris l'École médicale de Harvard. Actuellement, la plupart des facultés de médecine aux États-Unis utilisent l'APP dans l'enseignement préclinique (Kinkade, 2005). Comme approche pédagogique, l'APP a été mis en oeuvre avec succès dans diverses disciplines, telles que les sciences de l'infirmerie (Hodges, 2011), l'architecture (Maitland, 1997), les sciences de l'éducation (Duffy, 1994, Peterson et Treagust, 1998), les sciences (Duch, Groh & Allen, 2001), l'ingénierie (Fink, 1999 ; Woods, 1994) et la physique (Wiliams, 2001 ; Wiliams et Duch, 1997).
1.2. Qu'est-ce que l'apprentissage par problème (APP) ?
L'apprentissage par problème (APP) est une approche pédagogique selon laquelle les élèves peuvent apprendre à partir de situations signifiantes et réelles. Guilbert et Ouellet (1997) définissent l'APP comme un processus de résolution d'un problème complexe ou les participants regroupés par équipes, travaillent ensemble à la recherche des informations et à résoudre un problème réel ou réaliste proposé de façon à développer des compétences de résolution de problèmes et à faire en même temps des apprentissages de contenu. Cantin et al (1996) notent que l'apprentissage par problème vise à rendre opérationnelles les différentes connaissances spécifiques disciplinaires enseignées tout en ciblant d'autres objectifs de formation tels que l'autonomie, le développement des compétences de communication, de résolution des problèmes complexes réels, l'amélioration des stratégies de recherche documentaire efficaces ; l'apprentissage en groupe et enfin les transferts et l'intégration des connaissances. En APP, les élèves n'essaient pas de résoudre des problèmes hautement structurés qui les amène malheureusement à chercher la formule appropriée plutôt que de saisir les concepts sous-jacents. En APP, les élèves arrivent à comprendre le contexte réaliste qui leur est présenté et travaillent en petits groupes non seulement pour trouver une réponse, mais d'abord pour cerner la question à résoudre. L'APP exige que les élèves se répartissent les tâches entre eux et partagent leurs compétences. Les problèmes sont conçus pour permettre aux élèves de s'interroger et de travailler collectivement pour mieux comprendre la matière (Lasry, 2008). Gallagher et al. (1995) ont proposé quatre éléments essentiels pour l'APP qui doivent être groupés avec la pratique de la science : les problèmes devraient se focaliser sur les concepts scientifiques importants, il devrait y avoir des opportunités de tester les idées des élèves par une expérience au laboratoire ou sur le terrain, les élèves doivent gérer leurs propres données et enfin présenter leurs solutions. L'APP peut être appliqué dans les séances de travaux pratiques en adoptant des activités expérimentales afin de vérifier les solutions proposées. L'APP une alternative aux méthodes pédagogiques classiques car il peut résoudre plusieurs lacunes associées à celle-ci (Arnold, 2003 ; Hicks & Bevsek 2012 ; Kelly & Finlayson, 2007 ; Ram, 1999).
1.3. Pour quoi l'apprentissage par problèmes (APP) ?
L'APP est une approche visant à encourager les élèves à participer activement à la résolution de problèmes réels mal structurés. Apprendre en PBL est initié avec un problème (Gallagher et al, 1995) qui stimule les élèves à considérer ce qu'ils savent déjà et ce qu'ils vont explorer dans une investigation (Reynolds & Hancock, 2010). L'APP favorise également l'intégration des concepts et des compétences nécessaires pour la solution du problème et les élèves sont motivés pour étudier les problèmes réalistes qui sont susceptibles d'être intéressant pour eux. L'APP est une méthode d'enseignement centrée sur l'apprenant - réalisée individuellement ou en groupe - qui implique une étude indépendante, les discussions de groupe, la recherche, la réflexion sur la recherche et la présentation. En d'autres termes, les élèves doivent assumer la responsabilité de leur propre apprentissage et ils sont considérés comme des solveurs actifs des problèmes ainsi que des partenaires coopératifs avec les autres (Savin-Baden & Major, 2004). L'enseignant agit comme un guide et facilitateur pour aider les élèves à établir leurs objectifs, échafauder l'apprentissage et soutenir les processus de collaboration (Delisle, 1997 ; Hmelo-Silver, 2004). Des études ont montré que l'apprentissage par problème a des effets positifs à plusieurs égards. Notons une amélioration de la motivation des élèves à apprendre en leur donnant le contrôle et la responsabilité sur le travail qu'ils entreprennent (MacKinnon, 1999). Les élèves ont plus d'autonomie durant leur apprentissage, en particulier la définition de leurs objectifs d'apprentissage, la planification de leur apprentissage, l'accès et le choix de leurs propres ressources d'apprentissage et l'intégration de nouvelles connaissances dans la résolution de problèmes (Blumberg, 2000 ; Hmelo-Silver & Lin, 2000 ; Woods, 1996). L'APP responsabilise également la responsabilité les élèves pour trouver des informations, coordonner les actions et avec les collègues, atteindre les objectifs et contrôler la compréhension (Paris & Paris, 2001). Quelques études ont examiné l'efficacité de l'apprentissage auto-régulé dans un environnement d'APP bien que Sungur et Tekkaya (2006) ont rapporté que les élèves ont montré des niveaux élevés d'orientation intrinsèque des objectifs et de valeur de la tâche, une utilisation de stratégies d'apprentissage élaborés, une pensée critique, une autorégulation métacognitive et une régulation de l'effort par rapport à ceux du groupe témoin, qui ont été enseignées dans une approche traditionnelle d'enseignement. Lors de la résolution des problèmes non structurés, les élèves utilisent généralement leurs capacités de pensée critique pour analyser l'information et s'engager dans des processus métacognitifs tout en ruminant sur le processus de résolution de problème (Barrows & Myers, 1993). Par conséquent, l'APP a le potentiel de développer les capacités de réflexion plus élevées de contrôle, y compris la pensée critique et la pensée créative (Torp & Sage, 2002). Hmelo-Silver (2004) décrit l'APP comme une méthode d'enseignement où les élèves apprennent par la résolution facilitée des problèmes qui se concentre sur un problème réel et complexe. Les élèves travaillent en collaboration pour identifier ce qu'ils doivent apprendre afin de résoudre un problème, s'engager dans un apprentissage auto-guidé, appliquer leurs nouvelles connaissances au problème, et de réfléchir sur ce qu'ils ont appris et sur l'efficacité des stratégies employées. Torp et Sage (2002) décrit l'APP comme un apprentissage expérientiel concentré et organisé autour de l'investigation et de la résolution d'un problème réel et complexe qui n'a pas une réponse unique. Ils décrivent les élèves comme des solveurs engagés d'un problème, en cherchant à identifier la racine du problème et les conditions nécessaires pour arriver à une bonne solution, et dans un processus qui permet aux apprenants de devenir de plus en plus autonomes. Il s'agit d'une méthode d'enseignement pour un apprentissage tout au long de la vie.
2. Apprentissage par problème et technologies de l'information et des communications
Les ordinateurs ont montré un grand potentiel d'augmenter l'apprentissage des élèves s'ils sont utilisés convenablement, en tant qu'élément d'une approche logique d'enseignement (Bransford et al., 2000). Plusieurs recherches importantes (Bransford et al., 2000 ; de Jong et al. , 1998 ; Fiolhais et al., 1998 ; Jimoyiannis et al., 2001 ; McIntyre, 1998) ont étudié l'utilité pédagogique des logiciels éducatifs. Dans sa revue de questions sur les apports de la technologie informatique pour l'enseignement des sciences, Linn (2003) a abordé cinq principaux domaines dans lesquels ces technologies peuvent être utilisées comme support :
- des cours et des textes en sciences ;
- de la collaboration et des discussions ;
- de la saisie et la représentation des données ;
- de la visualisation de phénomènes scientifiques ;
- des modèles scientifiques et de la simulation.
Parmi les technologies les plus prometteuses en enseignement des sciences, on trouve la simulation sur ordinateur et l'expérimentation assisté par ordinateur. Elles sont devenues des ressources explicites pour l'enseignement de la physique.
2.1. Apports d'une simulation informatique
En enseignement des sciences, la simulation peut jouer un rôle important en créant des expériences virtuelles, permettant aux élèves de contrôler les paramètres, d'examiner de nouveaux modèles et d'améliorer leur compréhension intuitive des phénomènes complexes (Alessi & Trollip, 1985). Selon Roth & Roychoudhury (1993), les simulations peuvent activer les compétences procédurales de base des élèves en science, comme celles d'observer, de mesurer, de communiquer, de classifier et de prédire, ainsi que des compétences procédurales spécifiquement intégrées à la démarche scientifique, comme celles de contrôler des variables, de formuler des hypothèses, d'interpréter des données, d'expérimenter et de formuler des modèles. Selon Windschitl & Andre (1998), les simulations peuvent aussi contribuer au changement conceptuel et une étude de Zietsman & Hewson (1986) a montré que, si l'on tient compte des conceptions alternatives des étudiants, la simulation peut produire un changement conceptuel crucial chez eux. En effet, dans un environnement d'apprentissage constructiviste supporté par une simulation, l'insatisfaction surgit lorsque l'étudiant se trouve confronté à des résultats en conflit avec ses propres prédictions. En demandant aux élèves de faire et d'expliquer ces prévisions, on peut activer leurs connaissances antérieures et les forcer à élaborer des explications.
La prédiction, la manipulation et la vérification font une place importante au « discours interne » dans l'esprit de l'étudiant (Perkins & Simmons, 1988) ; en stimulant la vérification de l'hypothèse par l'étudiant, la simulation sur ordinateur permet de mettre en évidence un conflit conceptuel (Osborne & Squires, 1987) entre les hypothèses initiales et les observations (confrontation empirique), source d'insatisfaction intellectuelle. La résolution de ce conflit peut alors mener à une construction des nouvelles connaissances. Les simulations qui permettront aux apprenants de pratiquer la résolution du problème et de tenter ces solutions. Apprendre à résoudre des problèmes, il faut que les élèves soient en mesure de manipuler les éléments du problème et de tester l'impact du changement des paramètres qu'ils jugent importants pour formuler leurs solutions. Les simulations offrent aux élèves la possibilité d'interagir avec une représentation du problème. La forme de la simulation dépendre de la nature de l'activité conçue pour résoudre le problème. Les apprenants sont directement engagées par le problème qu'ils étudient afin qu'ils puissent faire une expérimentation et de voir immédiatement les résultats de leurs expériences. Cet engagement est mieux soutenu par des simulations de différents types. Selon De Jong & van Joolingen (1998), les manipulations sont déterminées par un modèle quantitatif ou qualitatif qui guide la simulation, le tâche principale de l'apprenant est d'en déduire, par l'expérimentation, les caractéristiques du modèle illustré par la simulation. Lorsque les apprenants interagissent avec la simulation, changent les valeurs des variables et observent les résultats, ils sont en train de tester leur compréhension du problème.
2.2. Expérimentation assistée par ordinateur (ExAO)
Si la simulation permet de manipuler les objets virtuels, l'expérimentation assistée par ordinateur perm et de manipuler les objets réels. Dans un environnement d'ExAO, les multiples capteurs sont reliés à une interface électronique qui communique directement avec un ordinateur. Ce dispositif offre à l'étudiant la possibilité de visualiser en temps réel le phénomène scientifique en concomitance avec sa représentation sous de multiples formes (Nonnon, 1986). L'apprenant est ainsi capable de créer des liens entre les multiples variables physiques étudiées. L'ExAO permet de réduire le temps consacré à la mise en place du montage expérimental ; à l'acquisition des données et à leur affichage ; à l'analyse de données expérimentales (Lazarowitz & Tamir, 1994). C'est aussi un outil didactique transversal puisqu'elle peut être appliquée de manière identique à plus matières (mécanique, électricité, etc.), mais aussi à plusieurs domaines (physique, biologie, chimie, technologie, etc.). En libérant l'élève de certaines taches telles que l'acquisition de données, Mc Corduck (1985) suggère que les apprenants ont des opportunités plus grandes d'employer un niveau plus élevé de stratégies cognitives lors de la résolution de problèmes et du développement conceptuel.
2.3. Simulation et ExAO
Dans cette étude, nous tentons de combiner certains avantages de l'ExAO à d'autres des simulations. Dans un premier temps, l'élève utilise l'ExAO pour analyser le mouvement d'objets sur une séquence vidéos, d'en extraire rapidement les graphiques de la position, de la vitesse, de l'accélération, de la force et de la trajectoire du mouvement. L'élève peut ensuite ajuster les paramètres pour tenter reproduire le mouvement en utilisant la simulation. La comparaison des résultats obtenus à partir de l'ExAO avec ceux obtenus par la simulation permet aux élèves de chercher une solution adéquate au problème proposé.
3. Objectif et question de recherche
La présente étude vise à étudier l'impact de l'APP sur la compréhension conceptuelle des notions en mécanique newtonienne auprès des élèves marocains de niveau deuxième année baccalauréat scientifique. Cette étude met l'accent sur les questions de recherche suivantes : l'APP est-il plus efficace que les méthodes traditionnelles d'enseignement au lycée ? Y a-t-il des effets de l'apprentissage par problème intégrant une simulation et l'ExAO sur la compréhension conceptuelle de la mécanique ?
4. Méthodologie
4.1. Échantillon et conception de l'étude
L'échantillon de la présente recherche se compose de 190 élèves marocains au secondaire qualifiant de niveau deuxième année baccalauréat scientifique repartis en quatre classes avec des options différentes : sciences mathématiques (SM), sciences de la vie et la terre (SVT), sciences techniques (ST) et sciences physiques (SP). Chacun des élèves participant à l'étude est affecté de manière aléatoire à un deux de groupes : expérimental (n = 95) ou témoin (n = 95) comme l'indique le tableau I.
Tableau 1. Répartition des participants à l'étude.
|
Groupe |
SVT |
SM |
SP |
ST |
|
EXP |
CTRL |
EXP |
CTRL |
EXP |
CTRL |
EXP |
CTRL |
|
Nombre |
28 |
28 |
21 |
21 |
22 |
22 |
24 |
24 |
Quatre enseignants des sciences physiques ont participé à cette étude, chaque classe (témoin et expérimental) est sous la responsabilité d'un enseignant. Le processus de mise en oeuvre a pris 4 semaines et les pré-test et post-test ont été administrés respectivement avant la première semaine de l'expérimentation et après la quatrième semaine ; ils ont été complétés par les élèves dans un format de papier et crayon. Pour étudier l'impact de l'APP, nous procédons à la comparaison de l'enseignement traditionnel avec l'APP dans un cours de mécanique concernant les lois de Newton. En enseignement traditionnel, les élèves n'avaient pas de séance de laboratoire. L'enseignant propose au début du cours, un problème hautement structuré à propos du mouvement parabolique du ballon de basketball. Les élèves lisent attentivement l'énoncé du problème et cherchent des informations supplémentaires afin de mieux comprendre le problème. Ensuite, ils commencent à formuler théoriquement l'équation du mouvement du ballon en s'appuyant sur la deuxième loi de Newton. Finalement, les élèves appliquent différents formules théoriques obtenues pour répondre à (aux) question(s) demandée(s). Durant les séances de l'APP, le contenu est semblable à celui traité dans l'approche traditionnelle. Nous nous sommes inspirées du modèle du « Illinois Mathematics and Science Academy » (IMSA, 1996) pour élaborer la séquence d'apprentissage par problème en cinq étapes dans des séances de travaux pratiques en sciences physiques au lycée, comme indiqué sur la Figure 1.
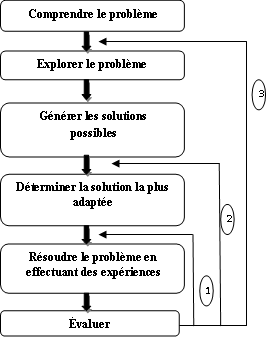
Figure 1. Séquence d'apprentissage par problème utilisée dans cette étude.
Dans la première étape, « comprendre le problème », l'enseignant présente l'énoncé du problème aux élèves et les invite à définir le problème et cerner les problèmes d'apprentissage en écrivant trois questions (KND) : « Que savons-nous ? » (K), « Que devons-nous savoir ? » (N) et « Comment pouvons-nous savoir ? » (D) (IMSA, 1996). Au cours les prochaines étapes « explorer le problème » et « générer des solutions possibles », l'étude du problème peut être soutenu par l'usage du matériel didactique et des outils informatiques (simulateur, ExAO par exemple) et les élèves doivent être en mesure de proposer un certain nombre de solutions possibles pour résoudre le problème. Aucune procédure expérimentale spécifique n'est fournie aux élèves. Il s'agit plutôt de les encourager à faire des recherches d'informations nécessaires pour sélectionner l'instrumentation appropriée, les méthodes et les procédures expérimentales pour résoudre le problème. Les élèves explorent les informations nécessaires et génèrent différentes solutions possibles en groupes. Pour déterminer la solution la plus adaptée, les élèves sont invités à réévaluer la validité et la faisabilité de leurs diverses méthodes proposées et sélectionner les meilleurs moyens pour résoudre le problème. Dans la phase finale, « résoudre le problème en effectuant des expériences », la solution du problème est étudiée en utilisant les moyens choisis les plus appropriés. Après avoir terminé l'investigation, les élèves, travaillant en groupe, analysent et évaluent leur processus choisi et les résultats obtenus. Quand les résultats de l'investigation sont jugés insuffisants, ils recommencent l'expérience (étape 1). Dans le cas où ils rencontrent des problèmes avec l'instrumentation choisie et la méthode d'analyse de la solution sélectionnée, ils optent pour d'autres solutions (étape 2). S'ils ont besoin de chercher une meilleure solution, ils peuvent revenir aux étapes antérieures (étape 3) pour résoudre le problème d'une manière plus appropriée.
4.2. Test FCI comme instrument de mesure
Nous utiliserons comme instrument de mesure un test largement diffusé dans l'enseignement de la physique aux États-Unis, le test Force Concept Inventory (FCI) développé par Hestenes et al. (1992). Il constitue, à l'heure actuelle, un des outils les plus utilisés pour évaluer la compréhension par les élèves des concepts de base de la mécanique newtonienne dans les cours de physique. Pour le FCI, les auteurs se sont inspirés des travaux sur les conceptions des élèves à propos du mouvement et de ses causes lors des entrevues ou des enregistrements de leurs réflexions personnelles lors de la passation d'un questionnaire ouvert. Son élaboration s'est étalée sur plus d'une dizaine d'années. Les réponses des élevés aux questions du FCI dans un format ouvert rapportent très bien à leurs réponses sur le format à choix multiples (Hestenes et al., 1992). Le test est consultable sur internet (le lien est indiqué dans la référence ( Halloun et al., 1995)). Selon ces auteurs, il est possible d'utiliser ce test comme outil de diagnostic pour identifier et classer des conceptions préalables aussi bien qu'un instrument pour évaluer l'apprentissage de la mécanique classique. Le test est considéré comme un bon indicateur pour jauger le degré de compréhension chez les élèves des concepts de base de la mécanique newtonienne (Hestenes et al., 1992). Le score d'un élève au test FCI est considéré par les auteurs comme une mesure de sa compréhension qualitative de la mécanique. Les auteurs indiquent qu'un score inférieur à 60 %, signifie qu'un élève n'a pas effectué la transition vers la pensée dans le paradigme newtonien, tandis qu'un score de 85 % signifie que l'élève est un penseur newtonien. Les auteurs suggèrent qu'un score de 60 % au test FCI constitue un seuil conceptuel pour développer une résolution efficace de problèmes en physique. L'instrument peut être utilisé sous forme de pré-et post-test dans un cours de physique pour déterminer l'amélioration de la compréhension conceptuelle des élèves. La FCI est composé de 30 éléments liés aux concepts de force et de mouvement. L'étude de la validité et de la fiabilité de l'inventaire pour l'échantillon de cette recherche sont menées par le chercheur. La FCI a été traduit en arabe et présenté à un groupe de physiciens et des membres du corps professoral de langue arabe. En utilisant les évaluations des experts, la version de la FCI a été révisée et administré à un groupe de 59 élèves marocains pour explorer leurs conceptions à propos les notions de la mécanique newtonienne (Droui et al., 2013). L'estimation de la fiabilité du test Kuder-Richardson 21 (KR-21) a été jugée de l'ordre de 0,71. Les données sont ensuite analysées avec SPSS 18.0 : le logiciel d'analyse statistique. Les moyennes et les écarts-types ont été calculés. Un niveau d'alpha de 0,05 a été utilisé dans toutes les analyses.
5. Résultats et discussion
En physique, les élèves peuvent être en mesure de résoudre plusieurs problèmes sans pour autant avoir une compréhension minimale de concepts de physique sous-jacents (Kim et Pak, 2002). La compréhension conceptuelle des élèves a donc été mesurée avant et après l'expérimentation à l'aide du test FCI (I. A. Halloun et al., 1995 ; Hestenes et al., 1992). Le tableau 2 résume les statistiques descriptives des scores au test FCI (variable dépendante) entre prétest et post-test des deux groupes. Nous pouvons constater que la moyenne des pourcentages du total de bonnes réponses du groupe témoin passe de 18,49 % à 31,73 %, soit une amélioration de 13,24 % tandis que la moyenne des pourcentages de bonnes réponses du groupe expérimental passe de 16,95 % à 47,25 %, soit une amélioration de 30,31 %.
Tableau II. Statistiques descriptives.
| |
Pré-test |
Post-test |
|
Groupe |
N |
Moyenne |
Écart type |
Moyenne |
Écart type |
|
Témoin |
95 |
18,49 % |
7,65 % |
31,73 % |
21,91 % |
|
Expérimental |
95 |
16,95 % |
7,79 % |
47,25 % |
24,60 % |
La figure 2 présente l'évolution des scores moyens obtenus des deux groupes : expérimental et témoin, avant et après l'expérimentation.

Figure 2. Évolution des résultats du FCI
Les résultats d'apprentissage conceptuel ont été également analysés en comparant les résultats des tests avant et après. Pour éviter les effets « plafond » ou « plancher », les gains conceptuels furent normalisés et comparés. Les gains normalisés (Hake, 1998) sont définis comme suit :
g = gain brut / gain maximal possible = (Post T – Pré T) / (max T – Pré T).
Cette mesure donne le rapport du gain conceptuel brut (post-test et pré-test) obtenu par rapport au gain maximal possible. Par exemple, un gain de 0,4 signifiera que 40 % des concepts restants à apprendre furent acquis à la fin du cours. Le gain normalisé est la mesure la plus fréquemment utilisée pour rapporter des résultats du FCI. Le tableau III montre les résultats moyens obtenus au test FCI par groupe avant (prétest) et après (post-test) l'expérimentation ainsi que les gains normalisés. Des tests paramétriques ont été utilisés pour détecter des différences significatives entre les résultats des groupes APP et traditionnel.
Tableau III. Résultats FCI en termes de gain normalisé d'apprentissage.
| |
Pré-test |
Post-test |
Gain normalisé |
|
Témoin |
18,49 % |
31,73 % |
0,16 |
|
Expérimental |
16,95 % |
47,25 % |
0,36 |
|
t-test |
1,378 |
4,713 |
5,184 |
|
Sig. (bilatérale) |
0,170 |
0,000 |
0,000 |
Ces résultats montrent que même si aucune différence significative n'existait entre les groupes avant enseignement (p = 0,17), le groupe APP obtient significativement plus de gains conceptuels (p = 0,000) après expérimentation. Nous marquons que la compréhension conceptuelle des élèves du groupe expérimental est meilleure que celle des élèves du groupe traditionnel, comme l'a montré le gain d'apprentissage conceptuel normalisé dans les scores FCI. La différence entre les résultats des deux groupes est très significative (t = 5,184, p = 0,000). Nous constatons que le gain normalisé d'apprentissage pour l'ensemble des questions, selon les indications de Hake, correspond à une amélioration moyenne et modérée du gain normalisé d'apprentissage pour le groupe expérimental (0,36) et un gain qualifié de un niveau faible (0,16) pour le groupe témoin. Ce résultat confirme que l'APP est plus efficace quant à l'apprentissage conceptuel que l'apprentissage traditionnel et, de ce fait, reproduit les résultats préalables des études de Mazur (1997) et Hake (1998).
6. Conclusion
Selon la littérature mentionnée ci-dessus à propos de la physique, la présente étude a révélé des résultats positifs soutenant en partie les résultats des études précédentes (Mazur, 1997 ; Hake, 1998). En outre, les résultats sont significatifs pour l'étude de l'efficacité de l'approche APP sur la compréhension conceptuelle de la physique newtonniene. Grâce à son attrait, nous croyons que la méthode de l'APP pourrait modifier en douceur la façon dont les enseignants et les élèves perçoivent l'enseignement.
Mohamed Droui 1, 2, 3, 4
Abdelkrim El Hajjami 1, 2
Mohamed Bouklah 5
Salaheddine Zouirech 1, 2
1. Laboratoire « Technologies de l'Information et de la Communication pour la Formation en Sciences », École Normale Supérieure-Fès, Maroc.
2. Laboratoire Interdisciplinaire de Recherches en Didactique des Sciences et Techniques (LIRDIST). Faculté des sciences Dhar El Mahraz- Fès, Maroc.
3. LaREF-EST, Université Mohammed Premier – Oujda, Maroc.
4. Université de Montréal / Canada et Mati-Montréal /Canada.
5. Centre régional des métiers de l'éducation et de formation - Oujda, Maroc.
Cette contribution est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification) <http://creativecommons.org/licenses/by-nd/2.0/fr/>.
Références bibliographiques
Albanese, M A & Mitchell, S (1993). Problem-based learning : a review of literature on its outcomes and implementation issues. Academic Medicine 68, 52-81.
Alessi, S. M. et Trollip, S. R. (1985). Computer-Based Instruction : Methods and Development. Englewood Cliffs, New Jersey : Prentice-Hall.
Arnold, R. J. (2003). The water project : A multi-week laboratory project for undergraduate analytical chemistry. Journal of Chemical Education, 80(1), 58–60, Awang & Ramly (2008)
Awang, H., & Ramly, I. (2008). Creative thinking skills approach through problem-based learning : and practice in the engineering classroom. International Journal of Human and Social Sciences, 3(1), 18–23.
Barrows, H. S., & Myers, A. C. (1993). Problem-based learning in secondary schools, (Unpublished Monograph). Springfield, IL : Problem-based Learning Institute. Lanphier high school and Southern Illinois University Medical School.
Blumberg, P. (2000). Evaluating the evidence that problem-based learners are self-directed learners : A review of the literature. In D. Evensen & C.E. Hmelo (Eds.), Problem-based learning : A research perspective on learning interactions (pp. 199–226). Mahwah, NJ : Erlbaum.
Bonate PL (2000). Analysis of pretest–posttest designs, Chapman & Hall/CRC, New York
Cantin, R., Lacasse, D. et Roy., L. (1996). Apprentissage par problème, activité de synthèse et épreuve synthèse. Pédagogie collégiale, 10 (2) : 5-10.
Delisle, R. (1997). How to Use Problem-Based Learning in the Classroom. Alexandria, VA : Association for Supervision and Curriculum Development,107 p., $12.95 paper, ISBN 087120-291-3.
De Jong, T. & van Joolingen, W. R. (1998). Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research, 68(2), 179-201.
Droui, M. EL Hajjami, A. Ahaji, K. et BenaliAmjoud, A. ( 2013). « The force concept inventory to explore a morrocan high school students' misconceptions about force and motion ». 5thWorld Conference on Educational Sciences, Roma. 05-08 February 2013.
Duch, B. J., Groh, S. E., & Allen, D. E. (2001). The power of problem based learning, Alexandria, VA : Stylus Publishing, LLC.
Duffy, T. M. (1994). Corporate and community education : Achieving success in the information society. Unpublished paper. Bloomington, IN : Indiana University.
Fink, F. K. (1999). Integration of engineering practice into curriculum : 25 years of experience with problem-based learning. Proceedings of the 29th Annual Frontiers in Education Conference.
Gallagher, S. A., Stepien, W. J., Sher, B. T. & Workman, D. (1995). Implementing problem-based learning in science classrooms. School Science and Mathematics, 95(3), 136–146.
Guilbert, L. & Ouellet, L. (1997). Étude de cas, Apprentissage par problèmes. Presses de l'Université du Québec, Ste-Foy, 136 pages.
Hake, Richard (1998). Interactive-engagement vs. traditional methods : A six-thousand-student survey of mechanics test data for introductory physics courses, American Journal of Physics, v66., p. 64-74.
Halloun, I., R. R. Hake, E. P Mosca, D. Hestenes. 1995. Force Concept Inventory (Revised, 1995),
[Online - password protected] at : http://modeling.la.asu.edu/R&E/Research.html
Hestenes D, Wells M, Swackhamer G (1992). Force concept inventory. Phys. Teach 30(3) :141–158.
Hicks, R. W., & Bevsek, H. M. (2012). Utilizing problem-based learning in qualitative analysis lab experiments. Journal of Chemical Education, 89(2), 254–257.
Hmelo-Silver, C. E. (2004). Problem-based learning : What and how do students learn ?. Educational Psychology Review, 16(3), 235–266.
Hmelo-Silver, C. E., & Lin, X. (2000). Becoming self-directed learners : Strategy development in problem-based learning. In D. Evensen & C.E. Hmelo (Eds.), Problem-based learning : A research perspective on learning interactions, (p. 227–250). Mahwah, NJ : Erlbaum.
Hodges, H. F. (2011). Preparing new nurses with complexity science and problem-based learning. Journal of Nursing Education, 50(1), 7–13.
IMSA. (1996). PBL network, collaborative inquiry in action.
Retrieved June 1, 2013, from http://pbln.imsa.edu/
Kelly, O. C., & Finlayson, O. E. (2007). Providing solutions through problem-based learning for the undergraduate 1st year chemistry laboratory. Chemistry Education Research and Practice, 8(3), 347–361.
Kinkade, S. (2005). A snapshot of the status of problem-based learning in U.S. medical schools (2003–2004). Academic Medicine, 80, 300–301.
Kim, E. et. Pak, S. J., (2002). Students do not Overcome Conceptual Difficulties after Solving 1000 Traditional Problems. American Journal of Physics, vol. 70, no 7, p. 759-765.
Lasry, N. (2008). Une mise en oeuvre au cégep de la méthode d'apprentissage par les pairs de harvard. Pédagogie collégiale vol. 21 no 4.
Lazarowitz, R. and Tamir, P. (1994). Research on using laboratory instruction in science, In D. L. Gabel Handbook of research on science teaching and learning. Maxwell Macmillan Canada, Toronto, p.94-128.
MacKinnon, M. M. (1999). Core elements of student motivation in problem-based learning. New Directions for Teaching and Learning, 78, 49–58.
Maitland, B. (1997). Problem-based learning for architecture and construction management. In D. Boud and G.
Mazur, E. (1997). Peer Instruction : A User's Manual, Upper Saddle River, NJ., Prentice-Hall.
Mc Corduck, P. (1985). The universal machine : Confessions of a technological optimist. New York : McGraw Hill.
Neild, T. (2004). Defining, measuring and maintaining the quality of problem-based learning [On-line].
Available from : http://auqa.edu. au/auqf/pastfora/2004/program/papers/Neild.pdf.
Accessed 1 june 2013.
Nonnon, P. (1986). Acquisition d'un langage graphique de codage pour la modélisation en temps réel de données d'expérience. Communication au 11e Psychological Mathematical Education Congress, Canada, Montréal
Paris, S. G., & Paris, A. H. (2001). Classroom applications of research on self-regulated learning. Educational Psychologist, 36(2), 89–101.
Perkins K. K., Adams W. K., Pollock S. J., Finkelstein, N. D., Wieman, C. E. (2005). Correlating student beliefs with student learning using theColorado learning attitudes about science survey. In : Marx J, Heron P, Franklin S (eds). Proceedings of 2004 physics education research conference, Sacramento, CA. American Institute of Physics, p. 61–64
Peterson, R. F., & Treagust, D. F. (1998). Learning to teach primary science through problem-based learning. Science Education, 82(2), 215–237.
Pundak, D., Rozner, S. (2008). Empowering engineering college staff to adopt active learning methods. J Sci Educ Technol 17(2) : 152–162
Raine, J., Collett, J. (2003). Problem-based learning in astrophysics. Eur J Phys 24(2) :41-46
Redish, E. F., Saul, J. M., Steinberg, R. N. (1998). Student expectations in introductory physics. Am J Phys 66(3) :212-224
Ram, P. (1999). Problem-based learning in undergraduate education. Journal of Chemical Education, 76(8), 1122–1126.
Redish, E. F. (2003). Teaching physics with physics suite. Wiley, New York
Reynolds, J. M., & Hancock, D. R. (2010). Problem-based learning in a higher education environmental biotechnology course. Innovations in Education and Teaching International, 47(2), 175–186.
Roth, W. M., Roychoudhury., A. (1993).The development of science process skill in authentic context. Journal of Research in Science Teaching, 30, 127-152.
Sahin, M. (2009). Correlations of students' grades, expectations, epistemological beliefs and demographics in a problem-based introductory course. In J Environ Sci Educ 4(2) :169–184
Savin-Baden, M., & Major, C. H. (2004). Foundations of problem-based learning, Society for Research into Higher Education. New York : Open University Press.
Sungur, S. & Tekkaya, C. (2006). Effects of problem-based learning and traditional instruction on self-regulated learning. The Journal of Educational Research, 99(5), 307-317.
Torp, L. & Sage, S. M. (2002). Problem as possibilities : Problem-based learning for K-16 education (2nd ed.). Alexandria, VA : Association for Supervision and Curriculum Development.
Vernon, D. T. A., Blake, R. L. (1993). Does problem-based learning work ? A meta-analysis of evaluative research. Acad Med 68(7) : 550–563Zietsman & Hewson (1986)
Windschitl, M. et Andre, T. (1998). Using computer simulations to enhance conceptual change : The roles of constructivist instruction and student epistemological beliefs. Journal of Research in Science Teaching, 35(2), 145-160.
Wiliams, B. A., and Duch, B. J. (1997). Cooperative problem-based learning in an undergraduate classroom. In A. P. McNeal and C. D'Avanzo (Eds.), Student Active Science : Models of Innovation in College Science Teaching. Saunders.
Williams, B. A. (2001). Introductory physics : A problem-based model. In B. J. Duch, S. E. Groh and D. E. Allen(Eds.), The power of problem-based learning : A practical "how to" for teaching courses in any discipline (p. 265). Sterling, VA : Stylus.
Woods, D. R. (1994). Problem-based learning : How to gain the most from PBL. Watertown, ON : Donald R. Woods.
Woods, D. R. (1996). Problem-based learning for large classes in chemical engineering. New Directions for Teaching and Learning, 68, 91–99.
|