|
« Une science encore incertaine » :
l'émergence de l'informatique
dans la recherche et l'enseignement supérieur français
Pierre Mounier-Kuhn
L'ordinateur et sa programmation remontent à la fin des années quarante. Ils n'ont été constitués en objets de recherches spécifiques qu'au cours des années 1960, en s'alliant avec la logique et d'autres branches du savoir. L'informatique n'a été reconnue comme discipline autonome qu'à partir des années 1970, au prix de vives controverses.
On peut décrire la montée en puissance de l'informatique depuis un demi-siècle comme une conquête appliquant une stratégie périphérique : existant à peine à la fin des années cinquante sous le nom de calcul électronique, technique auxiliaire de l'analyse numérique, cette profession embryonnaire ne pouvait songer à être représentée dans les instances centrales du pouvoir scientifique. Elle a donc commencé par se développer sur le terrain, dans les laboratoires, dans les enseignements annexes, dans diverses associations. Puis elle a organisé ses congrès, constitué des instituts, obtenu quelques chaires. Dix ans plus tard, la voilà reconnue comme discipline autonome au CNRS. Encore deux décennies, et elle conquiert des positions à l'Académie et au Collège de France [1].
Bien entendu cela n'est qu'une reconstruction de l'histoire a posteriori. Les proto-informaticiens, loin de méditer une stratégie aussi grandiose, faisaient simplement ce qu'ils pouvaient pour promouvoir des outils et des savoirs qu'ils jugeaient nécessaire au progrès des sciences et des techniques, dans un Enseignement Supérieur en expansion rapide. Comment en sont-ils arrivés à construire une science ?
Une nouvelle discipline peut résulter d'une théorie, ou bien d'une technique, notamment d'un instrument – ce fut le cas de la thermodynamique, puis de la radioastronomie. Elle peut naître suivant un processus de substitution, lors d'une révolution scientifique dont le modèle a été établi par Thomas Kuhn ; ou, plus souvent suivant un processus de spécialisation / spéciation par différenciation, comme une branche issue du tronc d'un arbre ; ou encore suivant un processus de convergence, comparable à l'hybridation qui crée une espèce vivante inédite, et impliquant la circulation et la traduction des concepts. L'histoire de la discipline informatique, aux étapes successives de son émergence, fournit des exemples typiques de ces différents processus.
En France, elle avait pourtant mal commencé. Alors que dans la plupart des pays industrialisés les premiers ordinateurs avaient été conçus dans des laboratoires universitaires, puis transférés à l'industrie, la France est le seul où la recherche publique ait échoué dans toutes ses tentatives pour en construire à l'époque pionnière de la « première génération ». Version peu enviable de « l'exception française » ! Ce sont donc des entreprises (SEA, IBM, Bull, Sneri...) qui développent et installent des ordinateurs à partir de 1955, dans les centres de calcul publics ou privés, apportant des moyens nouveaux à des activités préexistantes.
Les premiers numériciens
Depuis 1950 en effet, de jeunes professeurs de mathématiques se sont investis dans le calcul, à la fois par intérêt intellectuel et pour répondre à la demande de l'ingénierie électrique et mécanique. Dans quelques universités (Grenoble, Toulouse, puis Paris, Nancy, Lille et d'autres), ils créent des services de calcul, équipés d'abord de petites machines de bureau, ensuite de calculateurs électroniques. Aux cours existants de mathématiques appliquées, de probabilités ou de mécanique des fluides, ils ajoutent une spécialité qui est en plein renouvellement à l'étranger : l'analyse numérique, pour perfectionner les méthodes de calcul et les adapter à la puissance inédite des nouvelles machines [2]. Enfin ils constituent des équipes de recherche dans ce domaine, ce qui leur permet de former des assistants et d'obtenir des contrats pour financer des thèses et de nouveaux équipements. Un processus cumulatif de développement s'engage ainsi. Par effet boule de neige, en partant d'un seul maître de conférences (l'équivalent de nos actuels professeurs de 2e classe), on arrive en une décennie à des instituts de calcul numérique dépassant parfois la centaine de membres permanents.
Entre temps, suite au lobbying des universitaires modernisateurs qui s'activent sous le gouvernement Mendès-France, le Ministère de l'Éducation nationale a reconnu en 1956 ces enseignements en créant les premiers certificats d'analyse numérique au niveau licence et maîtrise, à Grenoble, Toulouse et Paris. Trois ans plus tard les premières chaires sont établies. Une nouvelle branche des mathématiques bourgeonne ainsi, avec sa société savante, sa revue trimestrielle, ses séminaires, puis son école d'été financée par l'EDF et le CEA. Si elle doit batailler pour faire admettre sa légitimité dans un milieu mathématicien dominé par Bourbaki, elle est fermement soutenue par des forces socio-économiques extérieures à l'Université. Dans les années 1960, ces cours se multiplient dans l'enseignement supérieur. Une véritable école française d'analyse numérique s'affirme et acquiert une stature internationale.
Les ordinateurs et leurs méthodes d'emploi n'ont alors que le statut d'une technique. Une technique de pointe au service des sciences, et qui pose des problèmes stimulants à l'analyse numérique. On bricole des outils de programmation – assembleurs, premiers langages évolués – qu'il faut adapter à l'architecture particulière de chaque calculateur. Quant aux réflexions « cybernétiques », ce bouillon de culture de la fin des années 1940, elles ont été repoussées hors du champ scientifique, dans le terrain vague des spéculations fumeuses.
Intérêts croisés
Pourtant des changements s'observent au début des années 1960. D'instruments scientifiques, les ordinateurs et leurs programmes deviennent aussi objets de recherches et d'enseignements théoriques. L'informatique va se constituer au croisement de savoirs et de projets très divers, qui s'y recomposeront. Aucune formation spécialisée n'étant disponible, les pionniers proviennent d'horizons variés – mathématiques, astronomie, électronique, voire philosophie ou linguistique – tout comme les premiers ordinateurs étaient assemblés avec des composants empruntés à diverses techniques préexistantes.
Le premier facteur de changement est le désir d'expérimenter, au-delà du calcul, des applications non numériques. Dès 1960 démarrent, au CNRS et dans quelques facultés, ainsi que dans les services de l'Armement, des recherches sur la traduction, la démonstration ou le raisonnement automatiques, la documentation par ordinateur, la reconnaissance de formes. Au même moment, un groupe international de mathématiciens conçoit Algol, un langage de programmation rigoureux, à vocation universelle, mais qui pose de redoutables problèmes d'implémentation concrète sur les machines tout en inspirant des réflexions fécondes sur les langages formels : Algol est non seulement un outil de communication, mais aussi un vaste programme de recherches [3].
Tous ces champs d'investigation se recoupent, ne serait-ce que parce que l'informatique est à l'époque un village de quelques centaines de personnes où tout le monde se connaît. Étudier la traduction automatique et les langages de programmation conduit à s'intéresser à une autre discipline, elle aussi en plein essor : la linguistique formelle, qui a d'ailleurs besoin des ordinateurs pour tester ses modèles, mais se fonde sur des mathématiques très différentes de l'analyse numérique – l'algèbre et la logique.
Précisément, la logique mathématique renaît en France après une longue hibernation. Quelques jeunes logiciens français ont découvert la machine de Turing, le lambda-calcul de Church et les théories de la récursivité une vingtaine d'année après leur invention [4]. Au début des années 1960, ils se rapprochent du milieu informaticien qui est de son côté à la recherche de modèles pour mieux comprendre ce qu'est un automate, un langage ou un algorithme. S'y ajoutent de multiples combinaisons avec d'autres sous-disciplines – la recherche opérationnelle, la combinatoire, la théorie des graphes... Naturellement, il faut quelques années de travail pour que ces rapprochements donnent lieu à de réelles hybridations de cultures et fassent germer, à leur tour, de nouveaux thèmes de recherches. Mais, dès le milieu des années 1960, c'est dans un tel humus que se forment par exemple les futurs concepteurs du langage Prolog ou des machines virtuelles.
Ainsi émerge une nouvelle communauté scientifique, par convergence d'intérêts, d'agenda intellectuels très divers, d'individus curieux et entreprenants. On y rencontre des managers de science, des geeks avant la lettre, des professeurs lumineux, d'autres obscurs, des personnalités originales, parfois carrément impossibles. Ils trouvent un terrain commun dans l'emploi de cette machine logique universelle qu'est l'ordinateur. Cette communauté scientifique a des dimensions à la fois locale (chaque équipe a son style, ses axes préférentiels, ses partenariats), nationale du fait de la spécificité du système scientifique français, et transnationale dans la mesure où se multiplient les échanges, les congrès, les réunions soutenues par l'OTAN ou par la fédération internationale des sociétés de traitement de l'information (IFIP), bientôt les migrations d'enseignants-chercheurs. Le mot informatique, inventé en 1962, tombe à point nommé pour désigner une profession nouvelle qui englobe, au-delà du calcul électronique, la gestion automatisée ou les recherches sur le traitement de l'information.
 | |
Figure 1. L'une des premières thèses d'informatique (1961).
| |
Assistante responsable des travaux pratiques de calcul à la faculté des sciences de Nancy, Marion Créhange soutient en 1961 une thèse que l'on peut considérer comme la première en France en « informatique » avant la lettre. Ce travail porte, non sur un sujet de mathématiques, mais sur la définition et la réalisation d'un macro-assembleur, d'un outil de programmation.
|
Le deuxième facteur de changement est la nécessité de mieux exploiter les ordinateurs. Ces machines sont très coûteuses et pour les rentabiliser il ne suffit pas de les faire fonctionner jour et nuit – ce qui n'est pas toujours possible dans certains locaux universitaires. Il faut aussi inventer des méthodes de programmation plus efficaces, élaborer des systèmes d'exploitation permettant de connecter plusieurs utilisateurs à la même machine (le time sharing est particulièrement intéressant pour les TP de programmation), étendre leurs domaines d'applications vers tout ce qui pourrait se « numériser ». Le développement de compilateurs, puis de systèmes d'exploitation devient un thème de recherches à part entière, occupant des équipes spécialisées subventionnées par les constructeurs d'ordinateurs ou par les agences gouvernementales comme la DGRST. Or, ces objets ne se rangent dans aucune discipline académique existante. Ils relèvent en grande partie d'une ingénierie experte, mais font appel aussi à des modèles mathématiques. Au-delà de leur statut épistémique, ils représentent un enjeu considérable à la fois pour les centres de calcul scientifique, ces grands équipements vitaux pour la compétitivité de la recherche, et pour les industriels qui sous-traitent ces développements aux laboratoires publics. Ces évolutions se marquent dans les changements de nom de la société savante, initialement vouée au calcul, qui adopte successivement les termes traitement de l'information, puis cybernétique économique et technique (AFCET) en fusionnant avec l'association des automaticiens.
 | |
Figure 2. TP de programmation à l'Université de Toulouse (1966).
| |
Dans cette salle de Travaux Pratiques, les étudiants apprennent « le binaire » sur des machines logiques conçues pour l'enseignement (plusieurs modèles de « calculateurs pédagogiques » ont été développés à cette époque dans l'industrie). Dans une autre salle, ils ont aussi accès à un ordinateur en temps partagé via des terminaux Teletype.
|
Le troisième facteur de changement est tout simplement la demande massive de programmeurs, d'analystes et d'ingénieurs informaticiens. Passant d'une centaine d'ordinateurs en France fin 1960 à plus de 3 000 en 1968, dont chacun nécessite une dizaine de techniciens en moyenne, le marché de l'emploi explose. L'enseignement supérieur peine à suivre, car il a trop peu d'enseignants spécialisés pour faire face à l'afflux d'étudiants. Pour former ces enseignants, il faut leur donner des sujets de thèses. Pour former ces étudiants, au-delà d'une initiation à Fortran, il faut élaborer des programmes de cours complets, formaliser les savoirs, donner des bases théoriques. Tous les domaines qu'explorent les équipes de recherche, de la logique et de la linguistique computationnelle jusqu'à l'analyse numérique et à la compilation, deviennent donc simultanément des matières de cours. Les certificats d'analyse numérique sont assez vite scindés en deux options : « Analyse numérique » et « Logique et programmation », deux disciplines qui se distinguent de plus en plus. Apparaissent les premières chaires professorales intitulées « Programmation », « Calcul électronique », voire « Informatique ».
On y enseigne ce qu'on a découvert six mois auparavant. D'où une atmosphère d'enthousiasme bouillonnant, sans laquelle les militants de l'informatique n'auraient d'ailleurs pu surmonter les mille obstacles levés devant une discipline qui veut conquérir sa place au soleil académique.
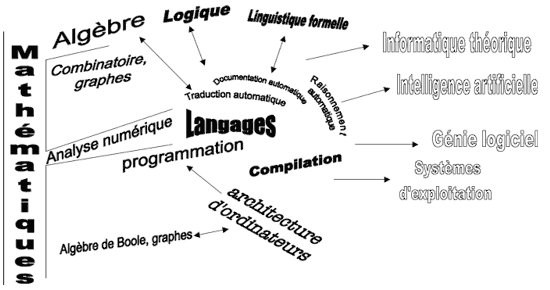 | |
Figure 3. Spéciation + embranchements + hybridations = convergences.
| |
Dans les années 1950, l'apparition des calculateurs électroniques stimule le développement de l'analyse numérique, la « mathématique du calcul ». Les numériciens élaborent des algorithmes qui doivent ensuite être codés sous une forme traitable par la machine : ainsi naît la programmation. Parallèlement, une toute autre branche des mathématiques, l'algèbre binaire, jusque-là purement spéculative, trouve une utilité pratique dans la conception des circuits logiques des ordinateurs. L'analyse numérique répond aux besoins de calcul et de modélisation de toutes les techniques, y compris chez les constructeurs d'ordinateurs.
|
Conquérir une place au soleil
Au milieu des années soixante, on commence à discuter du statut scientifique de l'informatique. Les archives livrent des controverses révélant incertitudes et antagonismes. Si l'informatique ne peut encore obtenir une instance d'évaluation autonome au niveau national, elle se renforce sur le terrain en devenant matière à diplômes spécifiques.
Au CNRS, on entreprend en 1965 de réviser le découpage des disciplines pour les adapter à l'évolution des sciences. L'essor du « calcul électronique » dans les laboratoires a conduit à une représentation croissante de ses spécialistes dans les commissions du Comité national, principalement dans la section de Mécanique générale et de mathématiques appliquées. La cohabitation de ces deux disciplines en pleine expansion étant devenue difficile, il y a unanimité sur la nécessité de les séparer et de créer une section vouée exclusivement à la Mécanique.
Mais quel statut donner à l'informatique, qualifiée de « science encore incertaine » ? Seule une petite minorité, appuyée toutefois par la direction du CNRS et par la DGRST, y voit une discipline nouvelle et souhaite lui attribuer une instance autonome. La majorité, notamment les mathématiciens les plus influents, juge préférable d'intégrer ce domaine dans la commission de mathématiques. Choix motivé à la fois par le désir de sélectionner plus rigoureusement « les chercheurs en analyse numérique » (on ne parle pas d'informatique) et par le souhait de sauver les mathématiques pures d'un risque de dessèchement en les irriguant de problèmes nouveaux.
C'est donc essentiellement une politique des mathématiques qui l'emporte sur le pari en faveur d'une science nouvelle. En 1967 et pour près d'une décennie, l'informatique au CNRS dépendra des mathématiques. Si elle n'y rencontre plus de concurrence pour ses budgets d'équipement (« les mathématiciens n'ont besoin que de papier et de crayons »), en revanche ses recrutements de chercheurs stagnent au même niveau que dix ans plus tôt. Activité interdisciplinaire, elle reste éclatée entre plusieurs commissions.
L'Université se montre plus ouverte, car elle doit répondre directement à la demande sociale. En 1966, la réforme Fouchet vise à créer des enseignements professionnalisants dans le cadre universitaire. Les informaticiens se mobilisent aussitôt et fondent une amicale pour présenter un interlocuteur collectif à la direction des enseignements supérieurs. Si, comme au CNRS l'année précédente, ils sont divisés entre ceux qui tiennent à conserver une légitimité mathématicienne et les militants d'une informatique autonome, ils parviennent à se mettre d'accord sur un tronc commun de programmes. En six mois, la licence et la maîtrise d'informatique sont mises sur pied, prêtes pour la rentrée 1966-1967. La même réforme crée les IUT, où les premiers départements sont souvent les départements d'informatique. Simultanément, les grandes écoles commencent elles aussi à se doter d'ordinateurs et à enseigner la programmation.
 | |
Figure 4. Une communauté constituée.
| |
L'école d'été d'informatique organisée par EDF, le CEA et l'IRIA, dans un château appartenant à Électricité de France, consacre sa première réunion en 1969 aux systèmes d'exploitation, avec des spécialistes internationaux tels E. W. Dijkstra et Brian Randell. On aperçoit aussi Louis Pouzin (1er à gauche au 1er rang), qui sera chargé deux ans plus tard de développer Cyclades, un réseau d'ordinateurs inspiré d'Arpanet. Et deux représentants de la génération suivante, qui pourront s'initier à l'informatique au lycée.
|
Le contexte politique favorise le mouvement : le Plan Calcul vient d'être lancé par le gouvernement. En créant l'I(N)RIA, qui amplifie les actions concertées de la DGRST, il affirme l'existence d'une recherche autonome en informatique et en automatique. Si la stratégie industrielle du Plan Calcul n'est guère convaincante, une partie importante de son action vise à rattraper le retard en matière de formation, notamment en implantant l'informatique dans tout l'enseignement supérieur. Des postes s'ouvrent partout au recrutement d'assistants et de maîtres de conférences, réclamant toujours plus de spécialistes. D'autres diplômes, comme les maîtrises d'informatique appliquées à la gestion (MIAGE), seront encore créés au début des années 1970, tandis que la jeune discipline commencera à s'introduire au lycée [5].
Ayant conquis ces positions et mettant les bouchées doubles pour faire face à la croissance rapide de la demande, les informaticiens (le mot est désormais d'usage courant) peuvent aller plus loin dans l'affirmation de leur discipline. Ils ont un allié politique à partir de 1970 : la Mission à l'informatique auprès du Ministre de l'Éducation nationale, dont le titulaire, Wladimir Mercouroff, est aussi chargé d'une mission similaire au CNRS.
Ils ont mûri leurs argumentaires. Un manifeste écrit en 1970 par le directeur de l'institut de programmation de l'Université de Paris, Jacques Arsac, s'intitule carrément La Science informatique. L'auteur estime que les relations entre les mathématiques et l'informatique doivent devenir similaires à celles qui existent entre les mathématiques et la physique. Dépassant le stade où l'on enseignait des recettes artisanales d'emploi des ordinateurs, amalgamant diverses disciplines et concepts autour de ses problèmes les plus intéressants, cette science nouvelle est essentiellement celle du traitement de l'information, avec ou sans ordinateur (ce qui se démarque nettement d'une computer science). Elle suit les étapes constitutives de toute science selon Claude Bernard : représentation du réel par un modèle formel, traitement par la théorie, interprétation du résultat. Science en construction, elle comprend des sous-disciplines qui se trouvent à différents stades de scientificité, et progresse vers un ensemble théorique cohérent et autonome. L'optimisme des formulations varie selon les auteurs et en fonction des images mentales qu'ils proposent de l'évolution d'une science.
Les discussions sur les programmes d'enseignement, dans le cadre des associations françaises comme des groupes de travail internationaux de l'IFIP, ont permis de mieux définir les contenus et les contours d'une nouvelle discipline. Centrée sur l'analyse des structures d'information, les concepts d'algorithmes, de machines et de langages, elle a des aspects fondamentaux ancrés dans les mathématiques, comme la théorie des automates ou le monoïde libre. C'est ce qui motive l'éclosion d'une informatique théorique, avec ses équipes de recherche, ses associations et ses publications spécifiques, au début des années 1970. L'informatique est en même temps une « science pour l'ingénieur » qui répond à une demande socio-économique pressante suscitée par des techniques évoluant à un rythme frénétique. Cette double identité coïncide parfaitement avec un souci grandissant, notamment au CNRS : afficher l'utilité de la recherche et créer un cadre pour promouvoir les « sciences de transfert ».
Les informaticiens académiques français peuvent aussi mettre en avant des réussites probantes – arguments plus forts que n'importe quel concept abstrait pour légitimer une activité, quelle qu'elle soit. Au début des années 1970, le langage Prolog, le système de bases de données Socrate, les innovations issues du centre scientifique IBM-IMAG à Grenoble, bientôt le réseau d'ordinateurs Cyclades et d'autres réalisations, montrent la rentabilité des investissements consentis depuis dix ans dans la recherche. Parallèlement l'école d'été de l'AFCET, créée en 1971, joue un rôle important dans l'émergence d'une science informatique, notamment pour aider les enseignants à construire des cours à l'époque où bien peu de matériels pédagogiques sont disponibles.
Une évolution décisive est la séparation, imposée par les autorités, entre les laboratoires d'informatique et les services de calcul. Si elle est douloureuse pour les chercheurs en informatique, elle empêche désormais leurs détracteurs de jouer sur la confusion entre les deux activités en les réduisant à leur aspect technique.
Enfin, les informaticiens peuvent maintenant s'appuyer sur l'argument du nombre : plusieurs centaines de titulaires de doctorats, des dizaines de chercheurs au CNRS et à l'IRIA, des assistants et des maîtres de conférences dans chaque université et dans chaque grande école – près de 270 enseignants-chercheurs de rangs A et B en 1971, analyse numérique non comprise. Il faut pouvoir les recruter, les évaluer, les représenter dans des instances scientifiques ayant leurs propres critères – et ne plus s'entendre objecter qu'une thèse d'informatique ne vaut rien car « elle ne démontre pas un seul théorème » !
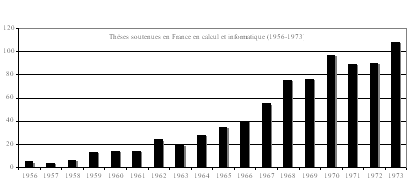 | |
Tableau 1. Nombre de thèses soutenues en calcul numérique et informatique (1956-1973).
| |
Notre recensement englobe tous les types de thèses. Partant d'une dizaine annuelle au début des années 1960, on dépasse la soixantaine en 1968, la centaine en 1973. C'est le « vivier » dans lequel se recrutent les enseignants, les chercheurs et une part croissante des informaticiens de l'industrie.
|
Vers une « science normale »
Fin 1970, une section a été créée au Comité consultatif des Universités, amalgamant l'informatique, la statistique et l'analyse numérique. Cette formule, qui aurait été satisfaisante cinq ans plus tôt, est dépassée. En 1972, une sous-section autonome est enfin attribuée à l'« Informatique fondamentale et appliquée », permettant aux représentants de la nouvelle discipline de définir leurs critères de scientificité et de coopter leurs candidats. Ce découpage demeurera jusqu'en 1983, où l'informatique recevra une section à part entière au CNU, toujours dans le cadre des mathématiques.
Au CNRS, l'autonomisation est un peu plus tardive pour de simples raisons de calendrier du renouvellement du Comité national, mais elle est plus radicale. En 1975, la création d'un département « Sciences pour l'ingénieur » permet de sortir l'informatique du périmètre des mathématiques et de l'associer dans une nouvelle commission avec l'automatique et le traitement du signal, eux-mêmes issus de la physique. Cette ablation ne se fait pas sans douleur, les mathématiques voyant leur échapper des ressources considérables et des problèmes intéressants. En résolvant le dilemme de la place de l'informatique, on en pose un nouveau aux spécialistes d'autres disciplines comme l'analyse numérique, qui se trouvent à leur tour écartelées entre deux sections. Des hommes qui ont joué un rôle décisif dans le développement du « calcul électronique » préfèrent rester électeurs parmi les mathématiciens et affirmer « l'unité des Mathématiques ».
Dans un paradoxe commun en histoire, c'est à ce moment que le rapprochement entre les mathématiques et l'informatique, souhaité dix ans plus tôt, devient visible. Les ordinateurs commencent seulement à atteindre une puissance permettant de vérifier des hypothèses ou des démonstrations de mathématiques pures. Ils suscitent le développement de nouveaux procédés comme le calcul formel. Enfin, les progrès de l'informatique permettent de développer, au-delà du calcul traditionnel, la simulation numérique qui relève à la fois du calcul, de la théorie et de l'expérimentation.
Plus généralement, l'emploi des ordinateurs qui touche maintenant toutes les branches du savoir, combiné avec l'établissement de la discipline informatique, entraîne une recomposition progressive du paysage scientifique.
Les activités naguère désignées par les termes analyse numérique ou recherche opérationnelle se redistribuent sous d'autres pavillons, algorithmique, modélisation et calcul scientifique, ou systémique. La catégorie mathématiques appliquées était une catégorie à la fois pédagogique et socio-professionnelle qui englobait traditionnellement la mécanique rationnelle, le calcul différentiel et intégral, les équations aux dérivées partielles, les probabilités et statistiques. Elle perd graduellement de son sens à mesure, d'une part que d'immenses pans du savoir, laborieusement apprises depuis le XVIIIe siècle par des générations d'étudiants, sont incorporés dans des logiciels de calcul, d'autre part que les applications mobilisent des mathématiques très variées, y compris celles qui étaient habituellement classées comme « pures ». Si, dans les années 1960, l'informatique était généralement considérée comme une branche des mathématiques appliquées ou une application des mathématiques, ce sont ensuite les mathématiques appliquées qui, ne pouvant plus se passer d'ordinateur, deviendront « une succursale de l'informatique » [6]. Enfin une nouvelle catégorie ad hoc apparaît, les « mathématiques discrètes » [7], fédérant les branches des mathématiques directement liées à l'informatique – mathématiques numériques, combinatoire, une partie de l'algèbre, de la logique et de la théorie des langages et de façon générale les mathématiques du discontinu – qui permettent de représenter l'ordinateur ou son fonctionnement et sont employées en modélisation. Cette catégorie offre une position alternative à celle de « science informatique ». Ce qui n'épuise pas pour autant les controverses sur le statut scientifique de la nouvelle discipline [8].
Au passage, l'étude de ces processus permet de tester le modèle élaboré par Thomas Kuhn dans La Structure des révolutions scientifiques : si, dans le cas de l'informatique, la notion de « révolution scientifique » n'est pas pertinente (l'ordinateur est d'abord une innovation d'ordre technique qui ne vise pas à renverser un paradigme), l'activité et le militantisme des chercheurs en informatique pour constituer et légitimer celle-ci correspondent exactement à ce que Kuhn décrivait comme « l'acheminement vers une science normale ». C'est une fois établie que l'informatique a commencé à transformer les autres disciplines, non seulement en les équipant d'ordinateurs, mais aussi en leur apportant des modèles au point que plusieurs d'entre elles se qualifient de computationnelles.
Jouant désormais parmi les sciences un rôle aussi central que l'analyse au siècle précédent, l'informatique est reconnue au début du XXIe siècle aux plus hauts niveaux institutionnels de la recherche française. Elle a une chaire au Collège de France, des fauteuils et des correspondants à l'Académie des sciences, un institut à part entière au CNRS qui collabore avec l'Inria. Certains de ses représentants sont présidents d'universités, ce qui aurait été impensable il y a trente ans. Avec 800 professeurs et 2 000 maîtres de conférence, cette « science en construction » est devenue la première discipline par le nombre d'enseignants recensés au Conseil national des universités.
Ce qui lui permet d'engager la bataille pour s'établir comme discipline dans l'enseignement secondaire [9]. Ce projet a germé dès l'époque du Plan Calcul et s'articulait avec la revendication des informaticiens dans l'enseignement supérieur. Le même Jacques Arsac, directeur de l'institut de programmation de Paris, qui en 1970 avait publié son manifeste La Science informatique, est à l'origine d'une première option informatique des lycées. Cet enseignement, avec ses hauts et ses bas, allait implanter progressivement la science informatique dans le secondaire : en 1992 il concernait 50 % des lycées. Supprimé à deux reprises en 1992 et 1998, il réapparaît maintenant sous une nouvelle forme [10], désormais avec l'appui de l'Académie des Sciences [11] : on ne saurait trouver meilleure légitimation !
Pierre Mounier-Kuhn
CNRS et Université Paris-Sorbonne
Chercheur associé au Centre Alexandre Koyré
Une première version, plus courte, de ce texte a été publié sous le titre « Comment l'informatique devint une science », dans La Recherche n° 465 de juin 2012, pages 92-94.
http://www.larecherche.fr/idees/histoire-science/comment-informatique-devint-science-01-06-2012-91081
NOTES
[1] P. Mounier-Kuhn, L'Informatique en France, de la Seconde Guerre mondiale au Plan Calcul. L'émergence d'une science, préface de Jean-Jacques Duby, Presses de l'Université Paris-Sorbonne, 2010.
[2] Pour une remarquable et stimulante synthèse sur l'histoire du calcul, voir G. Dowek, Les Métamorphoses du calcul : Une étonnante histoire des mathématiques. Éditions le Pommier, 2007.
[3] P. Mounier-Kuhn, « Programme de recherche et construction d'une communauté scientifique : le langage Algol et l'émergence de la discipline informatique (1958-1980) », Anglo-French Conference on Scientific Communication and its History, Communicating Science and Technology II: From the 15th Century to the Present, Oxford & ENS, 9-10 mars 2012 (sous presse).
Sur Algol 68, voir notamment L. Trilling, « Algol 68, une culture informatique perdue ? », Colloque sur l'histoire de l'informatique en France, Grenoble, INPG, 1988, Vol. 1, p. 447-453.
[4] P. Mounier-Kuhn, computationnelle « Logic and Computing in France: A Late Convergence », in L. De Mol, G. Primiero (eds.), AISB/IACAP World Congress 2012 - History and Philosophy of Programming, ISBN978-1-908187-17-8, 2012.
[5] Sur l'informatique dans le système scolaire, que je ne traite pas ici, voir les bons historiques publiés dans « Quelques jalons pour un historique de l'informatique dans le système éducatif français » :
http://www.epi.asso.fr/revue/histosom.htm.
Georges-Louis Baron, L'Informatique, discipline scolaire ? Le cas des lycées, PUF, 1989.
Bernard Dimet, Informatique : son introduction dans l'enseignement obligatoire, 1980-1997, L'Harmattan, 2003.
Enseignants et ordinateurs à l'aube de la révolution Internet. Le cas de l'Académie d'Amiens 1980-1997, préface de Michel Armatte, L'Harmattan, 2005.
[6] L'expression est du Grenoblois Jean Kuntzmann.
[7] Je serais reconnaissant à quiconque pourrait me donner des précisions sur l'apparition du terme « mathématiques discrètes », sur ses motifs et ses premières occurrences. Le journal Discrete Mathematics est fondé en 1971, mais ses éditoriaux sont muets sur la stratégie dont il est l'organe.
[8] Sur les différentes conceptions de l'informatique, voir F. Varenne, Qu'est-ce que l'informatique ? Vrin, 2009 ; et Du modèle à la simulation informatique, Vrin, 2007.
[9] Voir l'article en trois parties de Jacques Baudé (2010) : « L'option informatique des lycées dans les années 80 et 90 ».
http://www.epi.asso.fr/revue/histo/h10oi_jb1.htm
http://www.epi.asso.fr/revue/histo/h10oi_jb2.htm
http://www.epi.asso.fr/revue/histo/h10oi_jb3.htm
[10] Gilles Dowek, Jean-Pierre Archambault, Emmanuel Baccelli, Claudio Cimelli, Albert Cohen, Christine Eisenbeis, Thierry Viéville et Benjamin Wack. Informatique et sciences du numérique. Spécialité ISN en terminale S, avec des exercices corrigés et des idées de projets. Eyrolles, 2012.
http://www.epi.asso.fr/revue/lu/l1206l.htm
[11] Académie des Sciences, Rapport de la commission sur l'enseignement de l'informatique, mai 2013.
http://www.epi.asso.fr/revue/docu/d1305a.htm
|