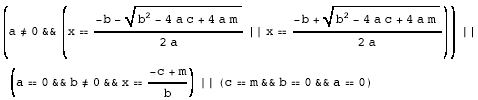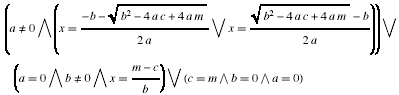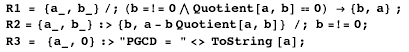|
Questions, Défis et Propositions Jacqueline Zizi L'informatique est une science naissante passionnante parce qu'elle a beaucoup de points communs avec les mathématiques, mais, par contre, elle a une dynamique très rapide et exponentielle. Tout le monde est concerné. C'est donc aussi un phénomène social nouveau. La structure de cet article épouse l'historique de la situation : évolution des machines, changement d'approche logicielle induite, propositions pour son enseignement, discussions des propositions existantes. Je terminerai par quelques-unes de mes propositions. 1) Machines aujourd'hui Aujourd'hui 26/09/2008, machines entrée de gamme pour le simple particulier Tableau comparatif des ordinateurs les plus modestes, premier prix, chez quelques grands constructeurs, à portée de beaucoup d'étudiants. Les éléments sont recopiés des fiches produits de ces machines trouvées sur Internet :
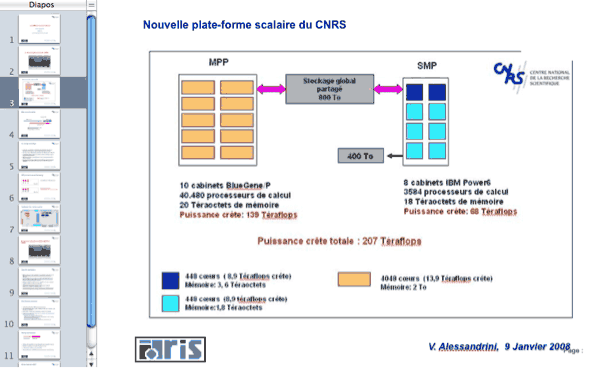
Donc ces machines intègrent toutes des processeurs à deux coeurs : Top machine pour la France L'IDRIS (http://www.idris.fr/) (Institut de Recherches et Développement en Informatique Scientifique) a été dotée de la plus grosse machine française : Blue Gene/P. Elle a fait ses premiers pas, calculs s'entend, au printemps 2008. Elle est arrivée 9e au Top-500 mondial de juin. Saluons la performance! Elle est constituée de 2 machines, une (MPP, ci-dessous) qui a 40 480 processeurs, l'autre (SMP, ci-dessous) qui en a 3 584, mais présente des caractéristiques différentes et intéressantes par ailleurs.
Cette copie d'écran invite à l'exposé de V. Alessandrini de l'IDRIS fait à la journée Blue Gene/P. C'était le 8 avril 2008 : « Le CNRS et le calcul intensif », une rencontre organisée à l'occasion de l'arrivée de Blue Gene. On trouvera le texte intégral sur le site de l'Idris. Pour l'état des lieux préliminaires, en 2006, on pourrra, par exemple, se rapporter à : Exercice : comparaison avec ces dernières années Faire un tableau synoptique des performances des pays européens (France incluse) au Top-500 ces dernières années. Puis discuter les résultats français. 2) Urgence logicielle Avenir Hard « La fin de la "Loi de Moore" se traduit par une prolifération des unités de traitement de l'information ("coeurs") dans les processeurs de base (...) Vers 2012-2015 on disposera de processeurs qui intègreront 124-256 coeurs » (V. Alessandrini) Pour la loi de Moore on pourra lire, par exemple : http://www.sciencepresse.qc.ca/node/18636 En 2012, même en admettant que le nombre de processeurs n'augmente pas, une machine à 45 000 processeurs pourra donc avoir plus de 11 millions de coeurs... OUPS...! Les calculs pour résoudre un problème pourront donc être distribués en même temps sur plus de 11 millions d'unités de calcul différentes. Mais une machine sans programme qui peut la nourrir et la faire travailler, c'est comme une voiture sans carburant. C'est pourquoi, le changement d'évolution matérielle induit un changement d'approche logicielle. « Le parallélisme massif, dans tous ses aspects (mémoire distribuée, mémoire partagée) est incontournable. » (V. Alessandrini) Avenir Soft La façon de procéder avec une machine est une chose, mais distribuer et gérer des calculs sur plusieurs machines pour traiter des problèmes complexes dont la nature n'est pas que séquentielle, en est une autre. Ici je voudrais juste donner une image. À table avec papa-maman et 2 enfants, on peut servir de façon tout à fait séquentielle avec un ordre que l'on aura choisi, l'entrée puis le plat principal, fromage et dessert. En admettant que tout le monde soit bien poli, le repas sera agréable. Et on peut même penser, qu'en plus, chacun peut être muni d'une mission comme mettre son assiette, verre et couverts dans le lave-vaisselle. Maintenant si on a 11 millions d'enfants, et que, en plus, il faut avoir fini de faire manger tout le monde au plus vite, faut-il avoir une seule personne qui servira l'un puis l'autre ? Probablement pas car un certain nombre d'enfants auront terminé l'entrée et voudront le plat principal avant même que toutes les entrées n'aient été servies. On peut alors penser distribuer les enfants dans des réfectoires avec des tables bien établies puis disposer de plusieurs personnes pour servir les tables. Les chances sont plus grandes de réussite. Mais si le serveur A a les 5 premières tables, puis un serveur B les 5 suivantes, etc. on voit tout de suite naître un problème, le jour où un des serveurs M, malade, au fond du lit avec 40° de fièvre, ne viendra pas, sans avoir pu prévenir. Tout le monde voit bien, d'ailleurs, aujourd'hui les « self » se multiplier dans les établissements scolaires, pour un service plus rapide. On remarquera que ces problèmes d'organisation, n'ont pas grand chose à faire avec la façon de cuisiner ce qui est servi pour chaque personne. De même, le risque de panne d'une machine est faible, mais il n'est pas nul. Gérer la distribution des calculs et le retour des résultats, en tenant compte des pannes éventuelles, ne s'improvise pas. Ces problèmes nouveaux, qui conditionnent l'ensemble, n'ont pas grand chose à faire avec la façon de calculer de chaque unité de calcul. Autrement dit la recette du chef et son savoir-faire, sont inopérants pour résoudre ces problèmes. En poursuivant l'analogie, se restreindre au fonctionnement d'une unité de calcul est inopérant pour la formation de nos futurs ingénieurs et scientifiques. On peut même se poser la question de savoir si cela est utile. Dans l'enseignement, une approche différente de celle que l'on pouvait avoir jusqu'à présent, lorsqu'on travaillait avec une seule machine, s'impose donc. Dans « Réflexions sur l'enseignement des sciences au lycée » rédigé par le Comité sur l'Enseignement des sciences de l'Académie des sciences : Et un peu plus loin, toujours dans le même texte : Questions - Quels sont les concepts de base à enseigner pour changer de cap logiciel dans l'enseignement ? - Qui va faire les cours d'informatique en lycée si une discipline nouvelle est créée ? Sur quel critère recruter ces personnes ? Comment les former ? En effet : « La question de leur formation est donc cruciale » (même texte, toujours) Défi Les machines sont là. Dans combien de temps, les décideurs se sentiront-ils prêts pour que TOUT : Une solution consisterait à faire que ces 3 pôles ne dépendent pas d'organismes différents, s'ignorant les uns les autres, voire s'opposant pour des raisons politiques. Aujourd'hui qui achète le matériel ? Dans les collèges ? Dans les lycées ? Qui achète les logiciels ? Qui nomme les enseignants ? Qui assure leur formation, iniale et continuée ? Où sont les ingénieurs système ? Comment et où un enseignant peut-il s'informer et surtout comparer sur le plan scientifique les solutions proposées ? Éviter les erreurs passées Il n'est pas le lieu d'entrer, ici, dans les détails de l'analyse de l'échec de la réforme de l'introduction des systèmes de calcul formel dans les programmes des classes préparatoires scientifiques. Toutefois, on peut remarquer, avec le recul du temps, en lisant les programmes et ses recommandations d'application, que ses rédacteurs étaient des précurseurs. Les causes de l'échec sont multiples. Voici une proposition de liste :
3) Proposition de Thierry Viéville Référence (i) « En classe préparatoire aux grandes écoles, le calcul formel ou symbolique est enseigné depuis plusieurs années. C'est un outil précieux en mathématiques. Il ne faut pas le confondre avec l'apprentissage de la programmation informatique. À ce jour, la mise en oeuvre de la programmation n'est pas séparée de l'utilisation du logiciel de calcul formel en tant qu'outil. » Thierry Viéville. (ii) « Adressons nous ensuite à l'autre génération, parfois bloquée par quelques idées reçues. C'est le démontage de ces idées reçues qui permet de lever les blocages pour que l'informatique trouve sa place naturelle. » Questions Q1- pourquoi le calcul formel ne serait-il qu'un outil ? Q2- pourquoi ne serait-il précieux qu'en mathématiques ? Un des points très forts de l'idée de cette réforme était justement de fournir un langage commun à des disciplines différentes. Q3- pourquoi ne pas confondre ? Puisque pour expérimenter il faut un langage de programmation, pourquoi ne pas exprimer dans ce même langage, concepts, apprentissage de la programmation et applications ? Q4- en classe prépas aujourd'hui, est-il vrai que « la mise en oeuvre de la programmation n'est pas séparée de l'utilisation du logiciel de calcul formel » ? Discussion Il suffit d'appliquer le démontage préconisé en (ii) aux affirmations faites ou sous-jacentes à celles faites en (i) pour répondre aux questions. Par exemple, pour Q4, la réponse est NON. La section suivante apporte un contre-exemple. 4) Avis de terrain, Marie-Aline Pery, commentaires Référence En cherchant dans ce texte le mot programmation, on le trouve intervenir deux fois : (iii) pour les prépas EC associé à des concepts informatiques : « instructions d'itération et de contrôle, algorithmes de tri » ; (iv) associé aux systèmes de calcul formel : « En classe scientifique hors option informatique, un peu d'algorithmique en première année, apprentissage d'un logiciel de calcul formel (Maple ou Mathematica) et programmation avec celui-ci. Discussion Cet avis est très intéressant. En effet : La première apparition (iii) est associée à une évaluation précise de concepts informatiques nommés. Elle se place dans un contexte du passé, dans un cadre très restreint, celui de la programmation procédurale, sans d'ailleurs comme nous le verrons, que ces concepts soient bien dégagés sur le plan mathématique ou sur le plan conceptuel. Quel sens leur donner sans une machine ? Ils sont d'ailleurs liés à un cadre très restreint : L'image citée est très pertinente et dénonce de façon imagée : Défis et Question
5) Conseil de Jean-Pierre Demailly, une question d'existence... Référence « je pense que l'éducation nationale aurait tout à gagner à préférer systématiquement les logiciels libres. D'une part, leur développement a atteint aujourd'hui un niveau tel qu'ils peuvent s'imposer comme une alternative crédible dans la plupart des domaines | souvent même comme une alternative techniquement supérieure aux offres commerciales. Coût du libre « En 2007, le marché français du Logiciel Libre a atteint un chiffre d'affaires de 730 millions d'euros. » Discussion La réforme des prépas a principalement échoué à cause de l'installation d'un monopole commercial. Un choix exclusif entre deux systèmes au lieu d'une ouverture au libre choix de la concurrence, a été une des facilités déterminantes offertes à ce lobby. On ne peut donc que souscrire à l'idéal de J.-P. Demailly de faire de la partie logicielle de l'informatique une sorte de mathématique ou tout serait gratuit. Et qui de plus est alléchante car elle se décline en « Open source », préludant l'ouverture. Mais hélas, cette proposition est elle-même basée sur un manque d'ouverture et prépare donc l'installation d'un autre monopole :
Question d'existence, défi Donner le nom d'au moins un logiciel libre qui soit : « une alternative supérieure aux offres commerciales » ou même plus modestement « crédible » et qui remplisse donc, au minimum, toutes les conditions suivantes :
Une preuve d'existence dans un autre monde En gras ci-dessous, on trouvera les questions et en dessous, en graisse normale, les réponses obtenues avec Mathematica : http://www.wolfram.com/. Ce qui prouve que dans le monde commercial, il existe au moins un système satisfaisant les 14 conditions précédentes. On trouvera ci-dessous en centré-gras les demandes faites à Mathematica et ses réponses, en dessous, en centré-normal. Justifiés à gauche, en petit ce sont des commentaires ou des explications. Exemple de (1), 3 petites questions : 102 345 678 903 568 054 205 685 899 999 562 431 879 235 413 295 468 297 213 500 687 + 2 1078 + 1 1078 + 1 == 1078 Exemple de (2), ces deux nombres sont - ils égaux ?
Comment - sont - ils vus en précision machine ?
Et en précision arbitraire ?
Exemple de (3), somme de 1 de 1 à N, pour N grand
Exemple de (3), suite récurrente B au départ, vaut 1 ; A vaut B + 1. Si x vaut 1, après 10 itérations de x → A x - B, que se passe-t-il ? Mathématiquement la suite des itérés est stationnaire. Tous ses termes valent 1. a) Cas où B est entier : B = 4095 A = B + 1 (A# - B) & [1] NestList [(A# - B) & , 1, 10] Ceci est la liste des résultats des itérés de cette fonction. Résultat normal. En mathématiques la fonction x → Ax - B peut aussi s'écrire # → A# - B. En Mathematica, le & indique une fonction, dont l'expression en un point # est ce qui précède le &. Donc (A # - B) & représente la fonction # → A# - B. NestList compose ici 10 fois la fonction précédente, avec pour élément initial le nombre entier 1. Clear [A, B, x] b) Cas où B est rationnel :
(A# - B) & [1] NestList [(A# - B) & , 1, 10] Clear [A, B, x] c) Cas où B est une valeur approchée, signalée par un point : B = 4095.1 A = B + 1 (A# - B) & [1] NestList [(A# - B) & , 1, 10] Pas de miracle, on travaille en numérique, en précision machine. Le résultat, faux, incontournable, correspond à l'érosion numérique signalée dans le site : http://www.lactamme.polytechnique.fr/Mosaic/descripteurs/FloatingPointNumbers.01.Ang.html. Clear [A, B, x] d) Une façon de faire pour obtenir un résultat numérique correct ? Calculer en exact puis passer au numérique, comme répètent tous les enseignants de physique tout au long de l'année.
(A# - B) & [1] Calculs effectués avec 50 décimales : N[NestList [(A# - B) & , 1, 10], 50] Clear [A, B, x] Calculs effectués en précision machine :
Clear [A, B, x] Une autre façon de faire, plus périlleuse, augmenter la précision des données : B est calculé avec 50 décimales avant tout :
Après 10 itérations, tout va bien NestList [(A# - B) & , 1, 10] Clear [A, B, x] Mais rien ne va plus pour 30 itérations, et même bien avant NestList [(A# - B) & , 1, 30] Clear [A, B, x] Exemple de (5) http://www.eprep.org/colloques/colloque08/communications08/Dieumegard_dia_1.pdf Exemple de (6) Cet article. Exemple de (7) Plus de 3 000 exemples de manipulations jouables avec MathPlayer, téléchargement gratuit, code aussi. C'est de l'Open Source avec pour langage de base Mathematica. Exemple de (8) x + x
Exemple de (9) Reduce [a x2 + b x + c == m, {x}] que l'on peut rendre plus habituelle avec un raccourci clavier par exemple :
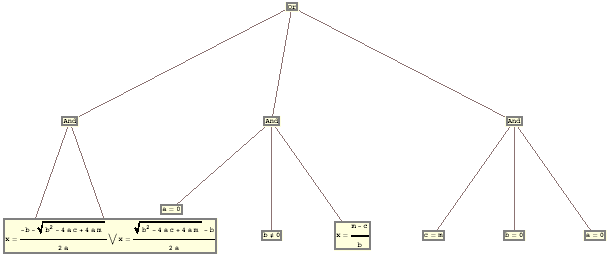
TreeForm [%, 2] De façon générale, pour un graphe, pas besoin de chercher une loupe, déplacez la souris au-dessus de ce que vous voulez lire et une petit boîte s'ouvrira avec un agrandissement de l'étiquette du noeud. Oui, en Mathematica les tooltips sont intégrés en standard. Pas d'erreur, le radical est bien interprêté, par exemple : Solve [ x2 + x + 12 == 0, {x}] Autre exemple où seuls les deux premiers niveaux de la structure sont mis en évidence :
Exemple de (10) Voici deux exemples, qui montrent ce que l'on pouvait faire, déjà, il y a plus de 5 ans : Dans ces exemples, et en particulier le second, très simple, tous les paradigmes cités, sauf procédural, sont représentés : L'exécution dépend des choix de l'utilisateur qu'il exprime en cliquant sur les boutons des palettes, exactement comme on le fait avec un Mac ou un PC aujourd'hui. Aujourd'hui, 5 ans après, ces exemples sont améliorables car il existe maintenant des possibilités offertes en standard pour représenter les sphères en 3D et faire du parallélisme. Exemple de (11) Le code HTML, XML, etc. lisible par les browsers du web, sont générés automatiquement par Mathematica par la demande Save As et le choix du format. Les références des paragraphes précédents en sont des exemples. Il en va de même pour TEX. Exemple de (12) Outre (7), et (10) ci-dessus, il suffit de lire la suite de cet article (section 7, 8, 9 et 10) pour en trouver des exemples. Exemple de (14) L'idée d'un cours dédié aux enseignants de prépa a fait son chemin et a laissé dans les divers colloques ePrep les traces de son évolution : http://www.eprep.org/ C'est une idée personnelle. Mon exposé au dernier colloque ePrep : En collaboration avec Wolfram Research, qui a assuré toute la logistique en particulier en faisant reproduire les fascicules d'accompagnement, la première séance gratuite de formation a eu lieu au lycée Fénelon à Paris et je suis heureuse d'annoncer que (14) est vraie. Toutefois il me semble fondamental de prendre le temps de faire bien. Mieux encore. Le premier niveau consacré à la manipulation directe est donc à ce jour, en réfection et en relecture, une fois encore, pour quelques jours. Les deux autres niveaux sont consacrés respectivement aux différents paradigmes de programmation et à la modélisation et direction de projets. 6) Associations EPI et ASTI, proposition de Gilles Dowek Référence Un seul document soutenu par ces deux associations, c'est la proposition de Gilles Dowek Ce document peut se trouver à une des adresses suivantes : Point de vue pratique au niveau des classes de lycée Page 6 de ce document, on lit : « 1. Programmation - En seconde et première. - En première et terminale. « 2. Algorithmique L'apprentissage des algorithmes de base doit être illustré par des exemples qui constituent autant de programmes que les élèves doivent apprendre à écrire (dans un langage largement diffusé, tels Pascal, Php, Ruby, C, Java). Les exemples de programmes illustrant ces algorithmes doivent être le plus attrayant possible. Ils peuvent être issus de problèmes venant d'autres disciplines. Ils peuvent aussi avoir une dimension ludique ou graphique. Voir en annexe une liste d'algorithmes proposés en classes de seconde, première, terminale. » Réinventer la roue ? Le préambule indique une volonté : « développera l'esprit d'initiative, de création. » Seulement les notions déclinées sont des grands classiques de l'enseignement de l'informatique en IUT, écoles d'ingénieurs, et Université. Et... Cependant on nous y invite, alors, pourquoi pas ? Ce document a le gros avantage d'exister et donc de servir de support à une discussion de fond. Je ne ferai ici que quelques remarques en m'appuyant sur 4 exemples de « notion » dont il est question : l'algorithme d'Euclide, la notion de boucle, les langages préconisés et les primitives graphiques. Chacun de ces exemples sera développé dans une des sections suivantes. 7) Algorithme d'Euclide Choix L'algorithme d'Euclide qui fournit le PGCD de 2 nombres, vient des mathématiques. Il est très ancien, donc a priori, robuste au changement de modes. Que va faire un élève ? Google → http://fr.wikipedia.org/wiki/PGCD → http://site2wouf.fr/calculator.php où on trouve en bas de page : Le compteur du nombre de visiteurs à ce jour est de 581294. (regardez à 2 jours d'écart, c'est impressionnant!) Donc, plus d'un élève va se dire : En faisant un pas de plus, on trouve d'ailleurs le source : Tout le devoir à faire par l'élève est donc là.
Pas bien difficile de le copier et de l'arranger un peu en changeant les noms de variable. Le devoir est bouclé. Au professeur de le corriger. Que peut faire le professeur ? S'il est consciencieux, il vérifiera, au moins déjà le résultat des tests, et il verra bien (s'il a un minimum de temps ou d'équipement) que le résultat de droite est faux. « C'est pas grave », puisque le logiciel est écrit en php et qu'il est « libre » = « Open Source » : Défis 1) En appliquant ce qui précède, trouver l'erreur dans le source et si on y arrive, compter le temps mis pour. 2) Multiplier le temps mis par le nombre d'élèves de la classe. Tenir compte du fait que d'autres peut-être auront choisi comme langage, Pascal ou un autre de ceux indiqués. Peut-il gagner du temps ? Si l'enseignant dispose d'un langage satisfaisant la condition (1), par exemple de Mathematica, il vérifiera facilement que : GCD [903 115, 87 624 545 862 548 796 532] et pourra vérifier un certain nombre de choses, comme : FactorInteger [87 624 545 862 548 796 532] Sinon que lui conseiller ? Faire les calculs à la main, semble la seule possibilité, mais pour le chronomètre... Un point de vue plus global, pour y voir plus clair Si l'enseignant a participé à une formation où son attention a été attirée sur la condition (1) du défi de la section 5, il regardera plus attentivement l'exemple. Il verra ainsi par exemple que dans le test de droite, bien que le nombre donné soit bien mémorisé, puisque affiché en bas de la page, il a été tronqué dès le début de l'application de l'algorithme. Pour des applications pédagogiques intéressantes Alors, le professeur pourra même donner des challenges aux élèves pour trouver des contre-exemples. Ce sera un terrain d'aventure indispensable pour la motivation. C'est un des moments privilégiés où on peut leur montrer l'importance de savoir/pouvoir travailler avec des grands entiers et ce que peuvent donner les égarements de leur remplacement par des « flottants ». C'est dans ces moments là qu'ils travailleront les concepts de PGCD, et peut- être de décomposition en nombres premiers. Et en démontant le code php que vont-ils apprendre ? Qu'est-ce qui va les motiver ? Vers d'autres sources de motivation et d'apprentissage Il faut réfléchir pour savoir si oui ou non étudier l'algorithme d'Euclide est utile. Supposons que oui. On vient de voir qu'on peut l'exploiter d'une nouvelle façon. Mais à condition d'avoir des moyens d'investigation fiables. Et pourquoi cacher aux élèves que c'est un grand classique et que dans ce domaine, les systèmes de calcul formel donnent directement la solution et des moyens de vérification ? N'est-il pas le moment de laisser libre cours à l'imagination des élèves pour aller plus loin ? Pour leur montrer que oui on peut faire avec des boucles, des tests, des affectations, « que les élèves doivent apprendre à écrire » et le touti. Mais non, on n'y est pas obligé du tout ! Voici une façon de faire :
euclide [a_, 0] := "PGCD = " <> ToString [a] Et en voici une deuxième :
Et une troisième :
Et une quatrième :
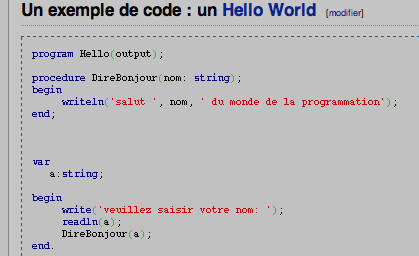
Remainder[a_, b_] := Mod[a, b] ; Et une cinquième : Onze lignes pour 5 solutions différentes et qui à elles toutes, ensemble, ont une écriture plus courte que le code source en php du programme fatidique. Cependant elles, elles donnent toutes un résultat correct sur le test : euclide[903 115, 87 624 545 862 548 796 532] pgcdR [903 115, 87 624 545 862 548 796 532] euclid[903 115, 87 624 545 862 548 796 532] EuclideanAlgorithmGCD [903 115, 87 624 545 862 548 796 532] {903 115, 87 624 545 862 548 796 532} //. {R1, R2, R3} En plus, elles font intervenir des concepts différents, polymorphisme, fonction récursive, fonctionnelle, fonction pure ou lambda fonction, règles de réécriture. La programmation par objets, m'est très familière (voir par exemple sur le site de EPI l'article Langages Orientés Objet que j'ai écrit, il y a 14 ans) mais elle ne me semble pas indiquée pour ce genre de problème (même si je vois bien dans le code php qu'elle y est présente, un marteau pilon pour écraser une mouche ?). Mais pourquoi pas, qui veut s'y essayer ? Toutes ces façons de faire, sans instruction, sans affectation, sans boucle, donnent un résultat correct sur l'exemple fatidique. Ce qui ne veut pas dire qu'elles sont toutes sans erreur ou optimisées. Ce qui pose beaucoup de questions : de la meilleure façon de faire, de la plus efficace, de la vérification et des tests qu'il vaudrait mieux faire, de la possibilité de créer encore, même en travaillant sur des grands classiques, etc. 8) Langages préconisés. Pascal, « largement diffusé » ? Pascal Les objectifs de la section II Programmation et Algorithmique, p. 5 du document EPI-ASTI, Gilles Dowek sont clairement exprimés : Programme simple n'étant pas défini dans la proposition discutée, et pas découragée par là où m'avait emmenée Google : « Même si le Pascal a eu son heure de gloire avec Turbo Pascal et les premiers Delphi, ce langage est actuellement en perte de vitesse. Les nouveaux programmeurs n'utilisent pas ce langage et les amateurs de Pascal actuels sont surtout des fans de la première heure. » J'ai pris le premier programme donné dans cette fiche Wikipedia :
J'ai écrit des centaines de lignes en Turbo-Pascal, donc pas très difficile de comprendre là où ils veulent en venir. Dans la foulée, j'ai alors écrit une petite phrase de Mathematica, la suivante :
que j'ai évaluée dans ce document, sans avoir à chercher un compilo et un éditeur, en appuyant sur la touche
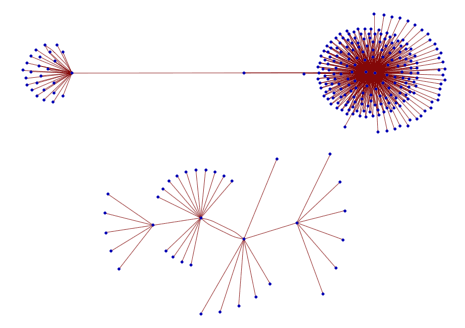
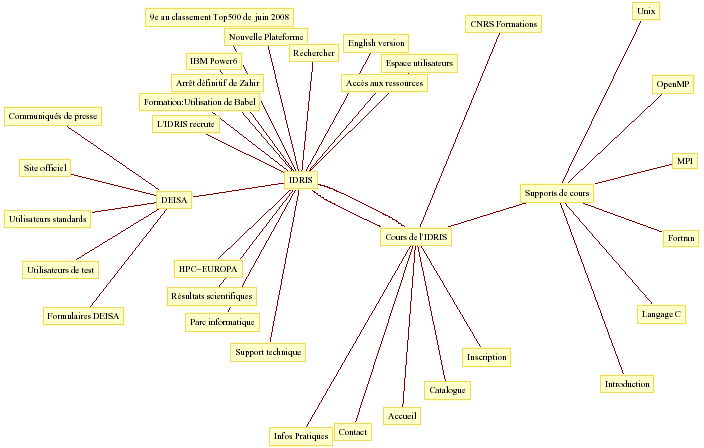
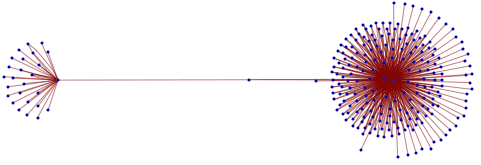
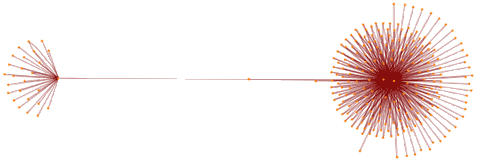
J'ai cliqué sur OK et voilà : Salut Jacqueline Zizi du monde de la programmation c'est le résultat d'une demande d'une ligne, que je ne qualifierai pas de « programme », dans un monde : celui de Mathematica. Et c'est le premier exemple de « programme » donné dans un autre : celui de Pascal. La question se pose donc bien de savoir ce qu'est un programme simple. Autre observation : Ruby, langage largement diffusé ? Qui, honnêtement, parmi les enseignants de prépa, par exemple, avant la lecture des propositions EPI-ASTI, Dowek, en a entendu parler ? Et pourquoi pas OCAML ? On trouve aussi l'algorithme d'Euclide, et traité de diverses façons en CAML : Ne serait-ce pas à cause de la phrase de conclusion concernant la solution procédurale de l'algorithme d'Euclide : 9) Boucle et ordre Et si on voulait définir ce qu'est une boucle ? Qui dit boucle dit ordre. Pour s'en convaincre on peut suivre le chemin : Définition d'une boucle : http://fr.wikipedia.org renvoie à structure de contrôle qui renvoie à instruction. Et pour instruction on trouve ici : Promenade libre Ce matin, j'ai navigué un peu sur Internet et j'ai noté les endroits par où j'étais passée et certaines directions qui s'offraient à moi. Voici le graphe support de ma promenade :
Peut-on ordonner cet ensemble ? Et pourtant, ce graphe renseigne bien sur ce que j'ai rencontré dans la promenade. De toute évidence je suis allée sur deux sites et je n'ai pas rencontré de lien de l'un vers l'autre. Il renseigne également bien sur la richesse et la structure des 2 sites sans que je n'ai eu à écrire une seule boucle. En quoi une boucle (ou même toute une famille de boucles) peut-elle m'aider ? Par exemple pour aller d'un point à un autre ? D'ailleurs, tout le monde sait comment trouver le code source d'un site à partir du menu de son browser Internet. Très bien. Décortiquons. Trouve-t-on dans le code source, par exemple dans le site EPI, celui du haut, une seule boucle ? Alors, sans instruction, sans boucle ni structure de contrôle ni déclaration, comment peut-on faire un tel dessin ? 10) Primitives graphiques Promenade sans ordre se programme tout simplement sans boucle Par un choix de structure des données. Par exemple, pour le site de l'IDRIS, sous forme de liste :
Puis, ce choix étant fait, pour plus de clarté, la définition d'une fonction : foo [{site_, liens_}] := Rule [site, #] & /@ liens Et le dessin, par application d'une primitive graphique : GraphPlot [Join[Flatten[Map [foo, data]]], VertexLabeling → True] Comment agit foo ? C'est simple, il suffit de lui demander : ? foo Oui, mais comment agit foo ? C'est simple, il suffit de lui demander : Map [foo, data] Elle transforme donc une structure en une autre structure. Et sans faire de boucle, eh oui ! Pour l'autre site, EPI Seules changent les données, que l'on structure de la même façon :
Et si on ne veut pas les étiquettes, on recopie ce qu'on a fait au-dessus, sans mettre l'option ; et voilà : EPI = GraphPlot [Join[Flatten[Map [foo, data]]]] On peut même définir en cours de route, si on veut, une variable globale, EPI. Et obtenir ensuite, par exemple si on n'aime pas le bleu, mais sans « l'affecter », un dessin avec des couleurs à son goût : EPI /. RGBColor[0, 0, 0.7`] → Orange et EPI n'a pas été modifié : EPI Questions Ainsi, chacun pourra faire son dessin, directement très vite, sans écrire de boucle. Alors se poseront les questions : et si on visite plusieurs sites ? Et si on va plus profondément dans le site, etc. Ouverture vers d'autres notions de représentation des données, par des listes, par des objets, etc. vers d'autres fonctions qui devront opérer sur ces ensembles nouveaux de représentation des données. 11) Constats et propositions Approche séquentielle versus parallélisme massif incontournable La dernière proposition EPI, ASTI, Gilles Dowek, se place pour les « notions » de base pour la programmation dans le cadre exclusif des langages informatiques procéduraux numériques. Ce qui induit de façon sous-jacente que le mode de raisonnement est celui d'un homme qui se met à la place d'une unité de calcul pour raisonner, avec un début, une fin une case mémoire fixe, etc. Ce qui formate l'esprit à un mode de pensée totalement séquentiel et ne me semble pas adapté à l'évolution logicielle incontournable annoncée. C'est également oublier la deuxième phrase du Comité sur l'Enseignement des sciences de l'Académie des sciences, « Ces concepts incluent bien sûr les algorithmes, les programmes susceptibles de les implémenter, les structures et le traitement des données. Ils s'étendent à des mécanismes logiques subtils comme la transposition en langage symbolique de la pensée universelle. », et qui conditionne, de mon point de vue, la réussite d'un enseignement de qualité pour demain. Donc dans la boîte temps allouée pour ces classes et cette discipline nouvelle, le programme proposé doit être taillé, précisé, émaillé d'exemples interdisciplinaires, de façon à garder sa place dans le « bien sûr » de la première phrase et surtout être complété par des propositions pour la deuxième. Ce qui suit concerne la deuxième. Symbolique La science informatique ne peut pas se passer du symbolique, comme les mathématiques. Confondre la mathématique avec les chiffres est très réducteur et n'a jamais servi de soc à l'enseignement des générations futures. Ce qui ne veut pas dire qu'on peut se passer des nombres et de leurs fascinants mystères. Au contraire. Des moyens logiciels puissants, sont à notre disposition pour mieux les comprendre. Seuls ces moyens ne peuvent rien. Mais les ignorer, c'est rester au moyen âge de l'informatique. C'est aussi se priver d'une façon actuelle disponible pour explorer certaines mathématiques et sciences qui les utilisent. Stratification, abstraction L'informatique, comme les mathématiques, est stratifiée en couches : le binaire, l'hexadécimal, l'assembleur, les langages procéduraux, les langages évolués qui génèrent des boucles et tests des langages procéduraux, qui eux même génèrent un code plus près de la machine, en sont des exemples. De même que les mathématiques à partir d'une axiomatique de base dans une théorie déterminée ont été complétées par la construction de théorèmes, puis de théories. Mais quels sont les mathématiciens qui, dans leur démonstration aujourd'hui, remplacent systématiquement tous les résultats connus par le décorticage systématique de tous les détails de preuve pour finalement ne citer que les axiomes de base ? Est-ce que cela serait même possible ? N'existe-t-il pas de nombreux articles qui ne les mentionnent même pas ? Et dans l'enseignement, commence-t-on en 6e par cette axiomatique ? Alors si on peut « faire directement » des mathématiques, pourquoi ne pourrait-on pas de la même façon « faire directement » de l'informatique ? Et dans l'enseignement de l'informatique, pourquoi faudrait-il ne faire que s'occuper de ce niveau le plus près de la machine ? Changement d'orbite Le moment est venu de changer d'orbite en informatique, de savoir utiliser ce qui est fait et de bâtir au-dessus sans revenir systématiquement aux couches les plus près d'une unité de calcul. La proposition EPI, ASTI, Gilles Dowek, s'appuie sur des exemples classiques. Nous avons vu, sur un exemple, la difficulté et les dangers lorsqu'on reste « le nez dans la couche » et tout au contraire la richesse de l'étude de ces exemples dans un cadre différent, où on peut prendre du recul par rapport à une situation, par abstraction. Les femmes On trouvera de belles références aux femmes dans l'article de Thierry Viéville, et des regrets pour le constat de leur présence (p. 7 de l'article : Réflexions sur l'enseignement des sciences au lycée). Décortiquer un objet logiciel pour comprendre, cela peut être, compte tenu des couches logicielles accumulées, long et difficile s'il est sophistiqué. Quels sont les hommes aujourd'hui qui démontent leurs bougies ou leur carburateur avant de prendre le volant ? Est-ce qu'on décortique un enfant pour le comprendre et l'aider à devenir un homme ? Qu'elle est la femme qui ne s'est pas émerveillée devant son bébé, lorsqu'elle vient juste d'accoucher ? Quelle est celle qui aurait eu envie de le désosser ? Beaucoup de femmes sont à l'aise dans les relations complexes et étudient les objets par les interactions qu'ils ont avec d'autres. Pourquoi pas ? Et n'est-ce pas une des raisons qui font qu'on les rencontre moins que les garçons dans les métiers de l'informatique, dont le vocabulaire actuel ressemble souvent trop à celui des militaires : commande, instruction, écrasement, procédure et autres déclarations ? Libres dans un joli cadre avec des règles du jeu connues, pas forcément obligées de faire une chose d'abord et l'autre après, pourvu que cela soit bien propre, bien fait, qu'on ne perde pas son temps et qu'on arrive au résultat. Oui je suis sûre que cela en tenterait plus d'une. Proposition pour la formation des professeurs de prépa Pourquoi commencer par elles/eux ? Parce qu'elles-ils sont au milieu du gué. Parce que c'est encore possible et à portée de main. Parce que la réforme qui a introduit le calcul formel dans leurs programmes, même si elle n'a pas été appliquée dans un esprit d'ouverture, même si elle n'a pas atteint les objectifs fixés, même si elle a été détournée, on ne peut plus « la remplacer » (cf. section 4). On peut par contre recibler l'application de cette réforme dans l'ouverture et lui donner les moyens de se développer. On ne peut pas revenir à l'âge de la pierre, chacun dans son coin. Comment ? Procéder par niveau et essaimage, dans le respect des choix de chacun(e) pour avoir un langage commun autour de sujets communs : C'est la proposition que j'ai faite aux colloques ePrep et qui a mûrie au cours des années. Cet article, comme mon intervention, aurait dû se focaliser sur ce dernier paragraphe. Elle n'est pas jetée sur le papier par hasard. Pour les raisons que j'ai déjà invoquées précédemment dans la section 5, il me semble plus utile d'élargir le débat. Depuis, j'ai fait une première séance de formation avec des professeurs de prépa (14) et j'ai lu d'autres articles que j'ignorais à l'époque. Il me semble donc plus important de dire ce que je n'ai pas trouvé ailleurs. Moyens ? Pour qu'une formation continuée ne soit pas décourageante, il est indispensable d'avoir des perches de secours, c'est-à-dire un endroit virtuel, site, forum de discussion, hot line, banque d'exemples, tenu de façon professionnelle, avec hébergement définitif et indépendant. Mais on a aussi besoin de lieux physiques : vitrine d'information, avec une permanence humaine fiable qui réponde aux questions posées. Et encore, et surtout, du temps. Et puis, une carotte : un merci, un bouquet de fleurs cela fait toujours plaisir et chaud au coeur. Pour le temps, en mathématiques, comme en sport, comme en informatique, il y a une part d'entraînement, d'acquisition d'automatisme et de bases. Personne ne peut l'acquérir à la place de l'autre. Il s'agit d'un effort personnel technique, d'acquisition des bases utiles. Cette partie de l'enseignement peut et devrait être automatisée, aussi bien pour l'acquisition que pour le contrôle. Elle dégagerait du temps pour les enseignants qui pourraient mieux se consacrer au reste. Des choses simples, directement accessibles, mais bien faites. Avec un contrôle impersonnel quantifié pour noter les progrès et encourager. Voici quelques exemples de sujets : résolution d'équations, de systèmes, calcul de dérivées, calcul d'intégrale, calculs de limites. Propositions pour les élèves On peut déjà à partir de là avoir un moyen de notation sur ces bases, sans risque de discrimination. Voire un concours. Organiser un concours informatique de programmation, avec de jolis lots, au niveau des classes de seconde/première/terminale, pour les élèves les plus motivés, avec une ouverture totale sur les moyens de résolution, mais avec des objectifs scientifiques très ciblés et beaucoup de rigueur dans la vérification des programmes. Avec bien sûr en préliminaire, des moyens (matériel et humain) mis à disposition pour leur préparation. Déjà, on pourrait leur demander, comme pour un anniversaire, ce qu'ils aimeraient, comme lot-cadeau. Proposition pour les enseignants-chercheurs Le niveau 1 de manipulation directe peut être acquise rapidement et seul par un universitaire qui a déjà l'expérience de plusieurs langages informatiques (TEX peut compter pour 1), s'il a une hot line fiable ou un environnement humain autour de lui, porteur. Pour les niveaux 2 et 3, par contre, un cours de formation leur ferait gagner du temps et donnerait une homogénéité et des repères sur le faisable facilement et sur ce qui risque d'être plus délicat. Donc plus d'efficacité. Cela éviterait aussi certaines dérives et pertes de temps dans une utilisation inadéquate. Réinventer la roue sans le savoir, jouer d'astuces non portables, accumuler des lignes de code en pelotes astucieusement imbriquées n'est pas la meilleure façon d'assurer un ensemble robuste, fiable et portable. La connaissance et l'utilisation d'autres voies ou d'autres moyens plus adaptés ne sont, hélas, pas forcément des préoccupations ressenties comme utiles. Et pourtant, elles favorisent le travail en commun, la formation des jeunes. Donc représentent un gain de temps important qui pourrait être occupé par ailleurs. Jacqueline Zizi jazi@club-internet.fr Le présent texte s'inscrit dans le cadre de la session 1 « L'informatique, une discipline à part entière ! Culture, fondamentaux et usages » du colloque international ePrep 2008. ___________________ |